课程环境：https://tai-e.pascal-lab.net/lectures.html

课程视频：https://www.bilibili.com/video/BV1b7411K7P4

南大《软件分析》15.0 CFL-Reachability and IFDS

这节课的内容比较难，理解起来比较困难，包括我自己，所以尽可能给出容易理解的解释。

在实际分析的过程中，一个控制流图会非常复杂，比如下图

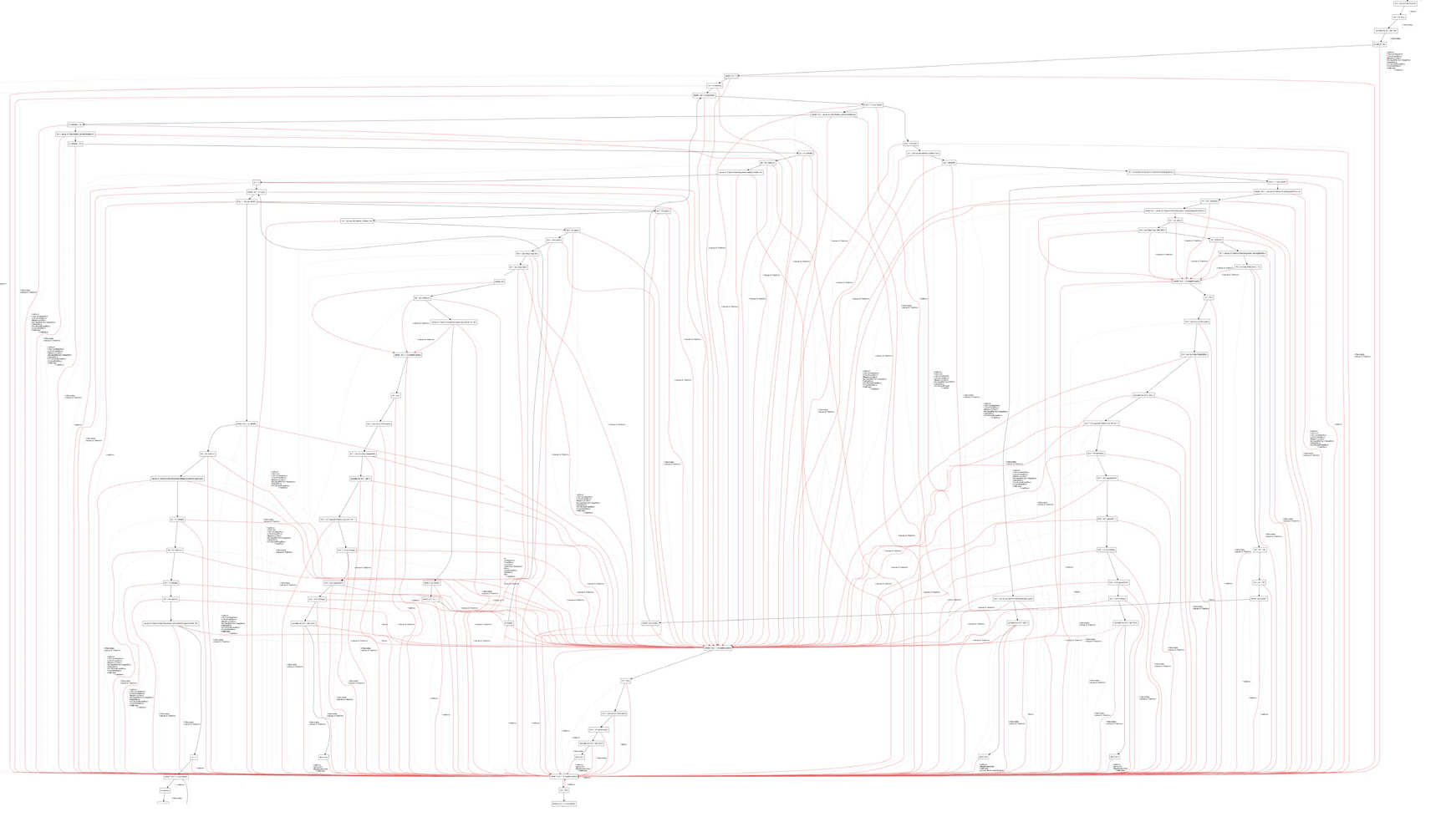
但这并不意味这张图里面所有的路径都会被执行（实际不会被执行的边称为 infeasible path），因此就产生了一个需求，尽可能通过一个may analysis 来判断一个边是不是 infeasible，从而来减少在程序分析过程中的误报，简单来说就是想让分析的结果更加精确。

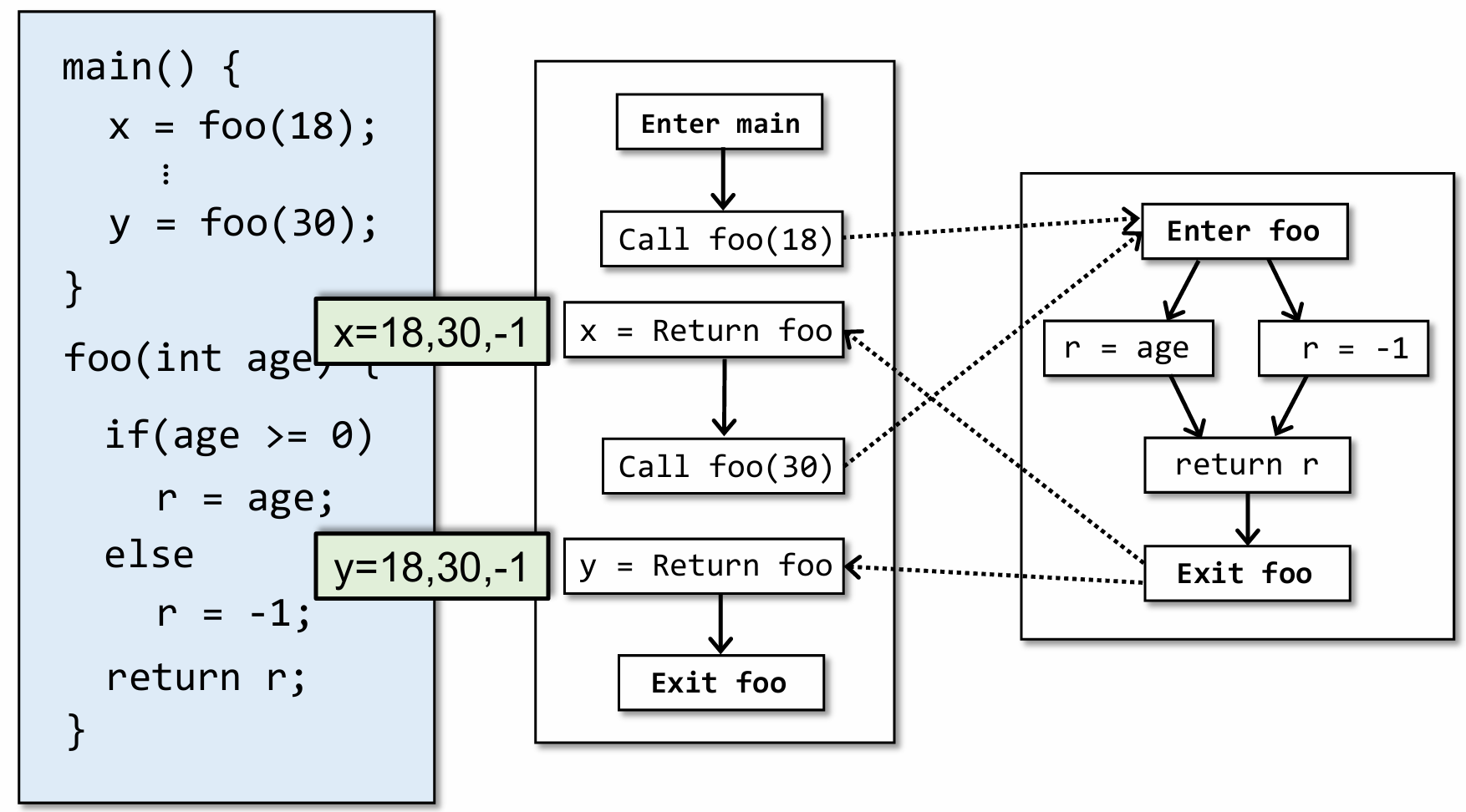
比如以上面这个程序为例，不考虑上下文敏感的过程间分析，最后常量传播的结果为绿色部分所示，其实我们知道结果完全可以更精确一点，即 x=18,-1 和 y = 30,-1，之所以造成上面的原因是因为静态分析将两次 call site 分析的结果没有区分直接进行了整合。而这一点是可以避免的，让结果更精确，这就是 IFDS 所要完成的目的

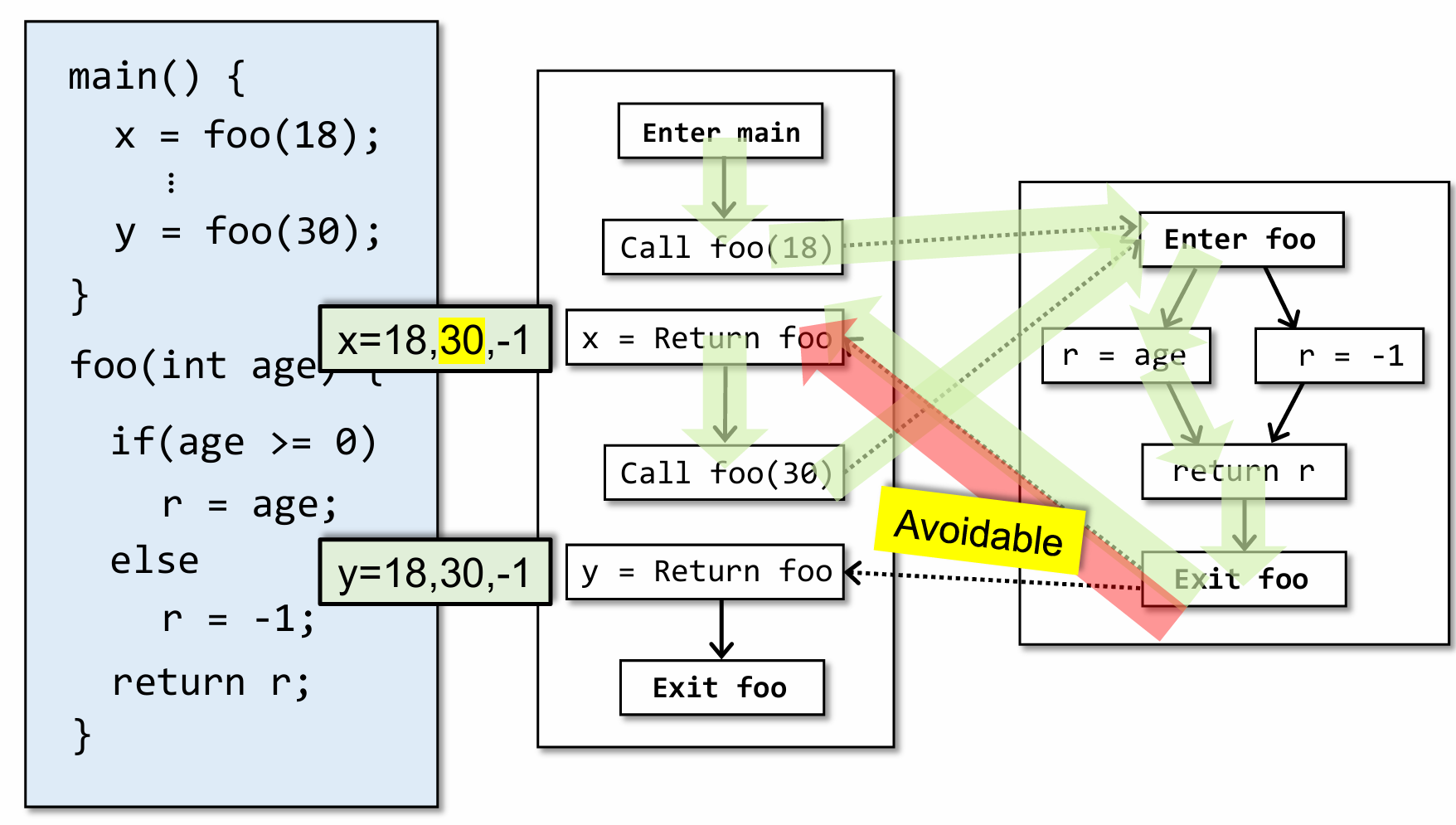
Realizable Paths

这里给出了 realizable path 的概念，其实就是我们前面提到的例子，剔除掉程序中的 infeasible path，那么剩余的 path 就是 realizable path。

注意事项：需要辨析的是 realizable path 可能会被执行也可能会不执行，但是 unrealizable path（infeasible path）一定不会被执行。

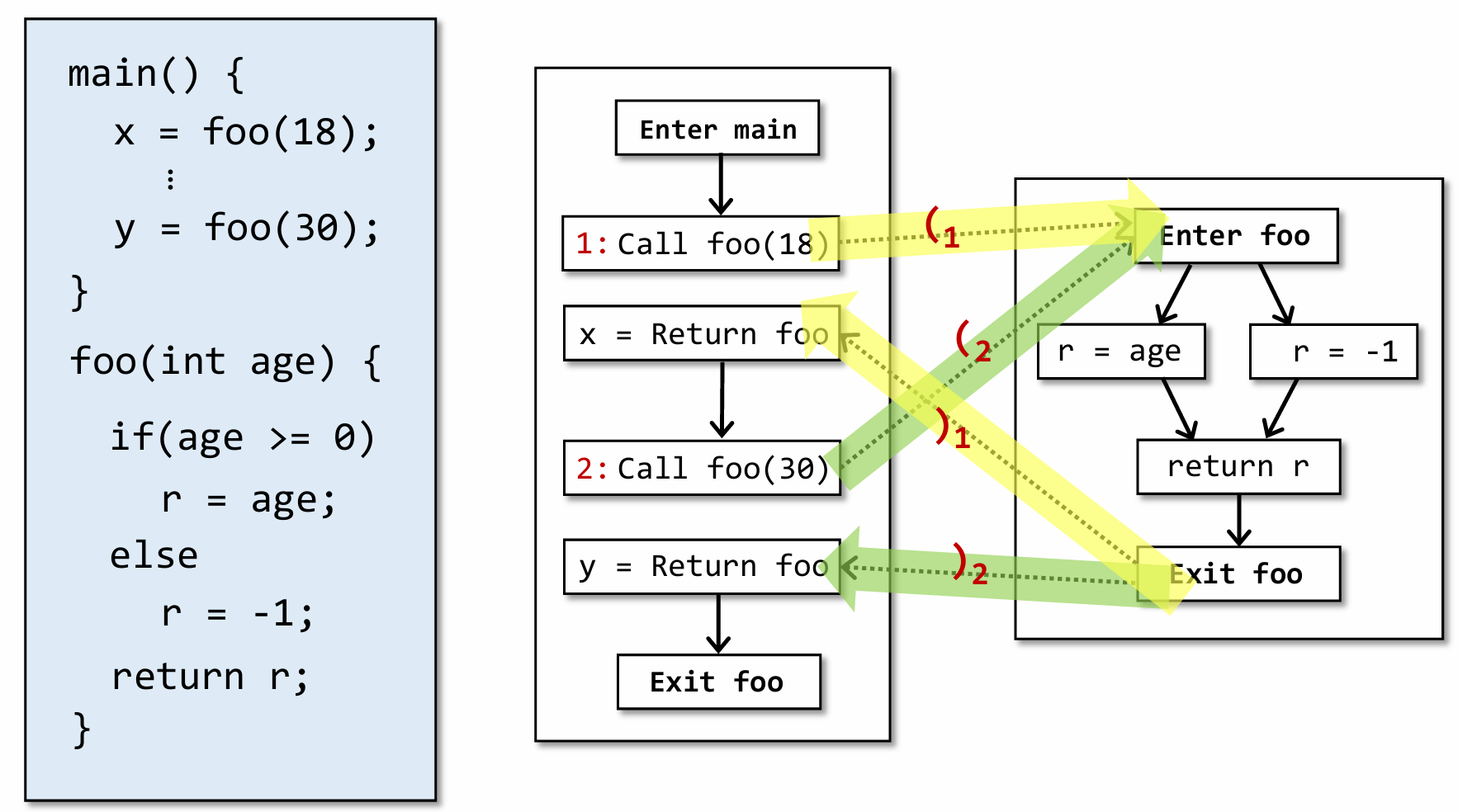
以前面的例子为例，我们要做的就是如上图所示，就像在上下文敏感技术中那样，尽可能让这些调用之间”隔离”，而做到这一点就需要引入 CFL-Reachability。

CFL-Reachability

与我们之前理解的可达性（reachability）不一样，不是说两个 node 之间有条路径就能满足了，还要满足上下文无关语法。怎么理解呢，将每一条边用一个”字母”来表示，最后通过 CFG 来检查这条路径上的所有边构成的”单词”是否满足特定语法，才能最终决定 A 是否与 B 之间是可达的。

CFG 的简单介绍如上，暂且先理解为其可以进行替换，即只要出现了 S，那么其就可以替换为 aSb 或者 ε。

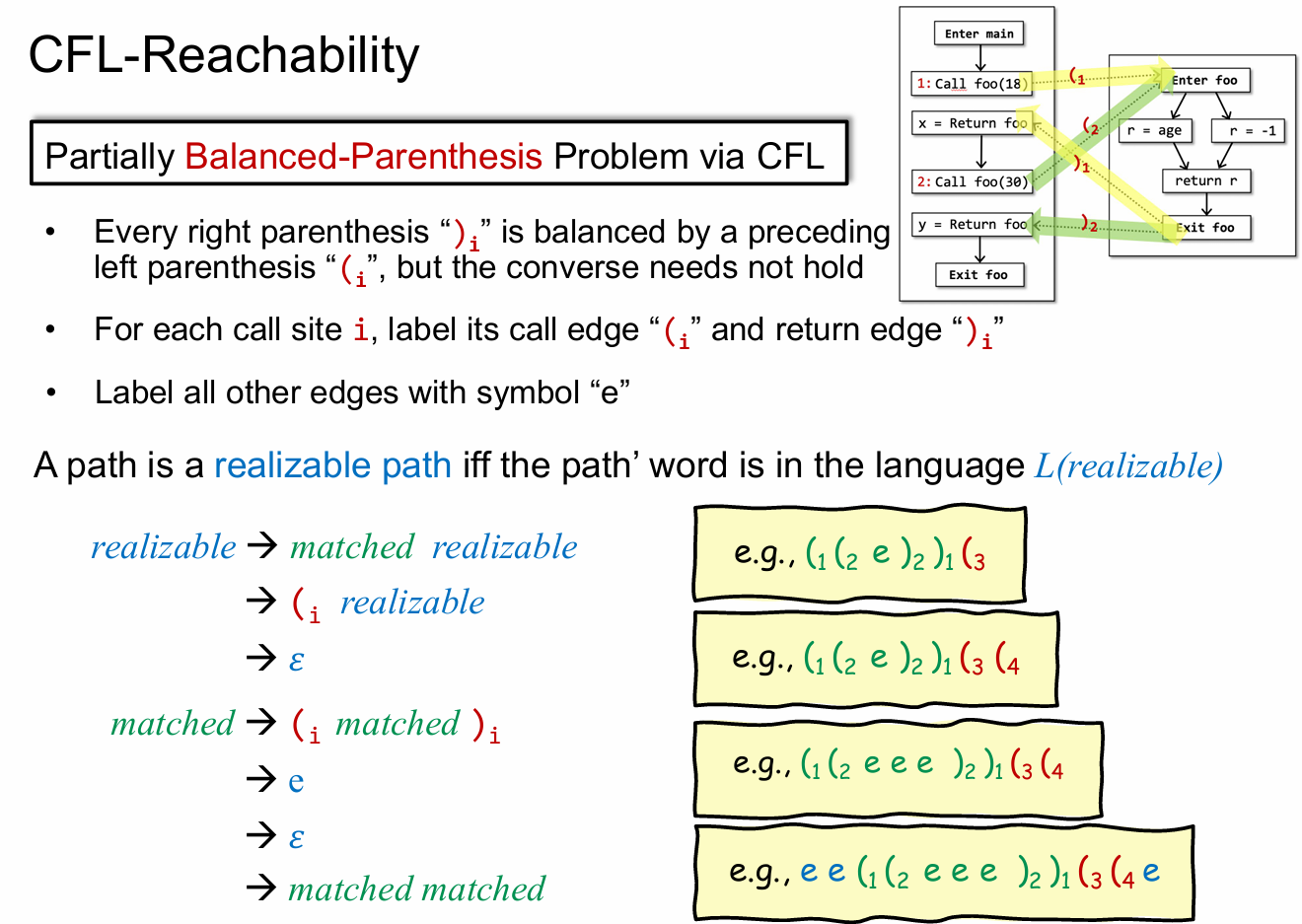
这一部分通过举例来说明部分括号匹配问题在 CFL 中的应用。

IFDS

其实这一部分，包括前面的部分，如果直接看理论会比较难理解，但这些其实都在为应用做准备，如果将例子理解的话（相对理论会容易理解些），就会同时理解前面的这些概念，所以说不要放弃。首先给出其概念

定义：IFDS 是基于有限域的（数据域是有限的，可以使用有限状态的表示和算法来处理数据流分析的问题），且数据流函数具有分配性质的过程间数据流分析。

指明 IFDS 研究范围是过程间的，有限的，满足分配的，子问题。

在前面的数据流分析中，我们有学过 MOP（“meet-over-all-paths），简单来说就是将每条路径上的结果到最后在一起汇总，那这里现在引入了 MRP（Meet-Over-All-Realizable-Paths），MRP 加入了 Realizable 这一性质，其实本质是一样的，不过我们这里只关注 Realizable path，因此与之相对应的方法就有了 MRP。

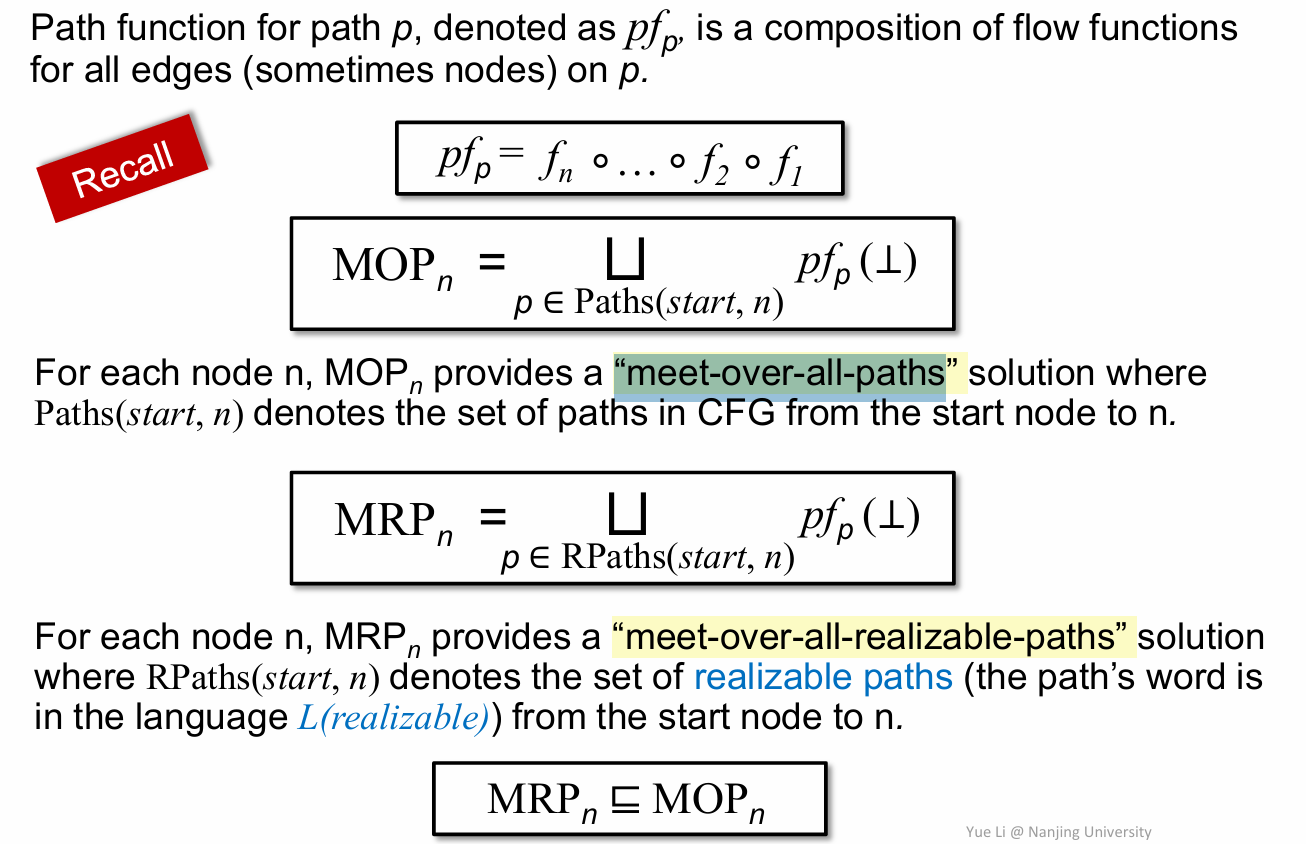
这里需要理解 flow function，在 IFDS 这一节中，我们在图上每条边上定义函数（后面举例会看到），这其实与之前的node差不多，只不过是以不同形式定义的，注意做好区分就行。

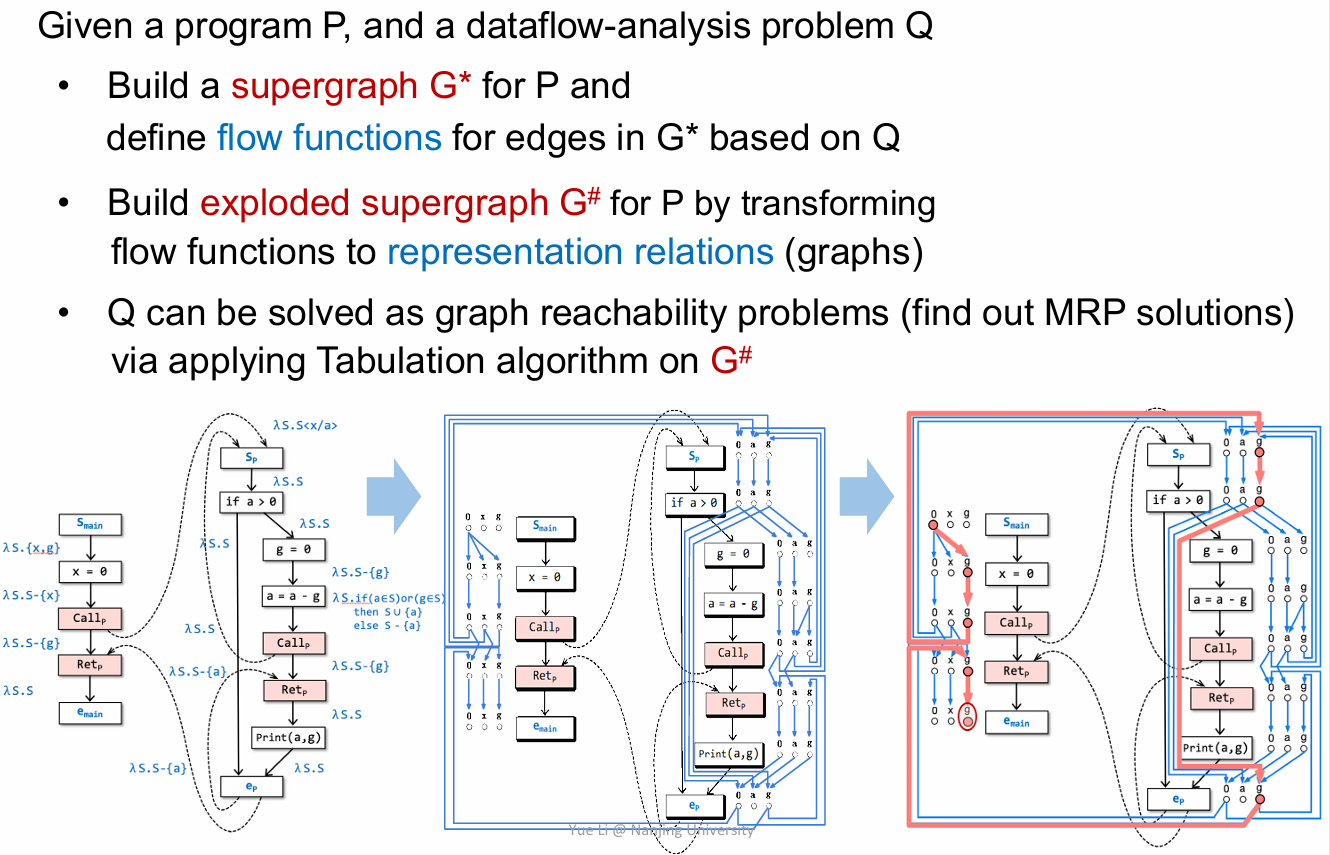
这张图给出了 IFDS 的过程，首先建立 supergraph G*，其次建立 exploded supergraph G#，最后对前面建立的G# 使用 Tabulation algorithm 求解可达性问题。

Supergraph G*

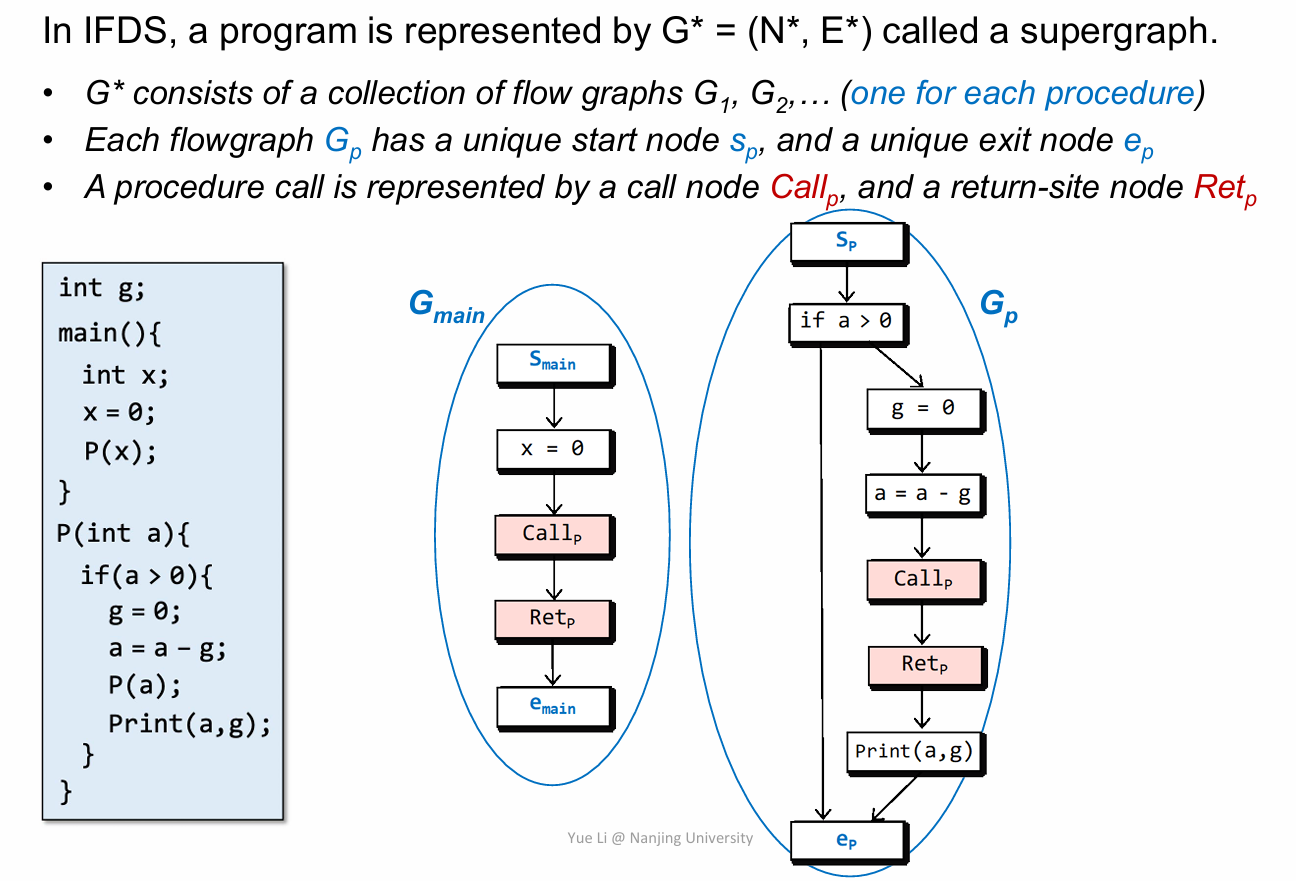
先来看看如何建立一个 Supergraph，前面两点都比较容易理解，需要注意的是第三点，在 IFDS 中，我们会将一个过程调用 call 用两个节点表示，一个叫做 call node，另外一个叫做 return-site node。

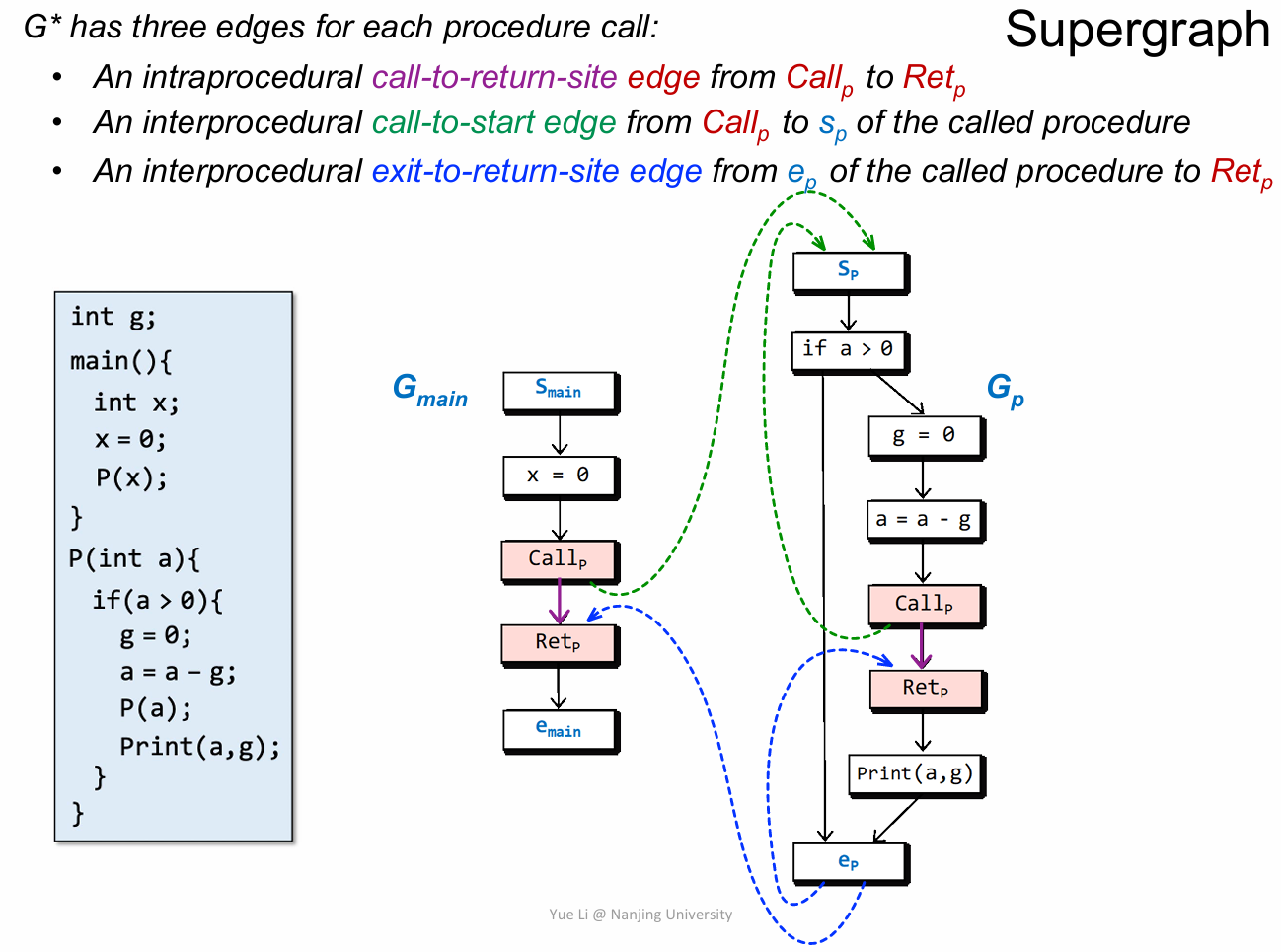
还有就是在 G* 中，要为过程调用引入三条新的边，分别为 call-to-return-site edge，call-to-start edge，exit-to-return-site edge。

还记得前面提到的 flow function 嘛，这里还要定义 flow function，在这一部分内容中定义如下：

“Possibly-uninitialized variables”: for each node n ∈ N*, determine the set of
variables that may be uninitialized before execution reaches n.

简单来说就是在到达 n 之前，没有被初始化的变量都有哪些。

还需要注意的就是，这种 λ . 的表达形式，比如说 λ x.x+1，前面的 x 是它的参数，x+1 是函数体（用花括号表示时代表输出）

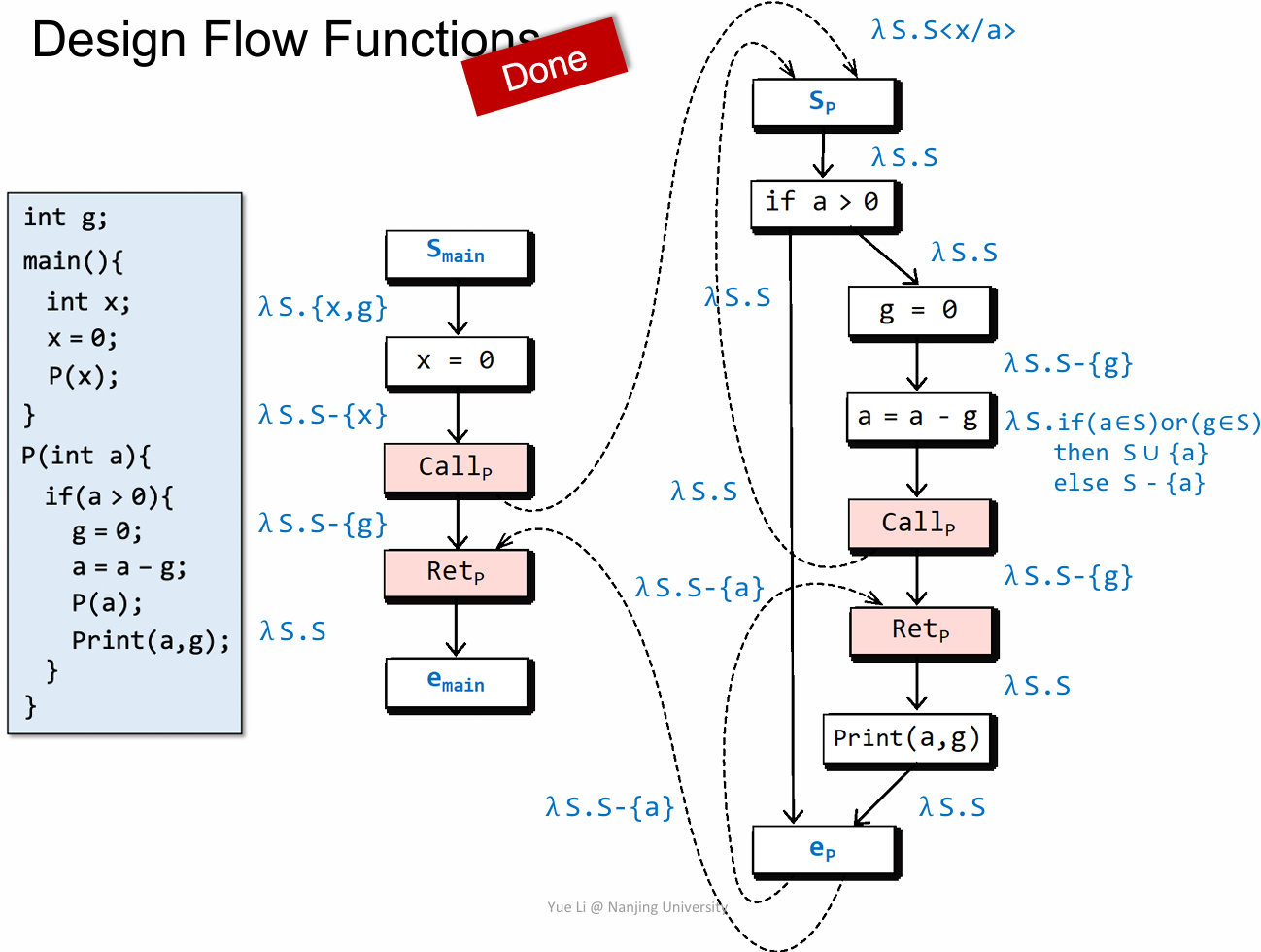
这就是根据我们前面对 flow function 的定义，最终得到的基于每条边的 flow function，最好能理解，看不懂也大概能体会到这个意思，这个 flow function 可以帮助后面建立 G#。

Exploded Supergraph G##

如上图所示，其实这个概念也相对理解起来有点抽象，怎么理解呢，就是说它把前面 G* 中关注的变量全部用一个 node 表示，如右上黄色部分所示，同时还引入了一个新的 node 0（后面会解释为什么需要一个 node 0），另外同时下面又有一排与上面一模一样的node。实际上 G# 做的事就是根据规则（）来处理不同排 node 之间的连接，同时可以注意到 给了三条规则，每条规则可以根据 flow function 来判断使用。

这里对每一条规则都进行解释（**理解了这个就理解了 G#**）：

{(0,0)} ：代表上一排 node 0 和 下一排 node 0 之间必有一条边

{(0,y) | y ∈ f(∅) }：代表当流函数没有输入时，如果总会输出 y，那么就建立一条从 0 到 y 的边

{ (x,y) | y ∉ f(∅) and y ∈ f({x}) }：代表当流函数有输入 x ，且 y 会被输出时，则建立一条从 x 到 y 的边

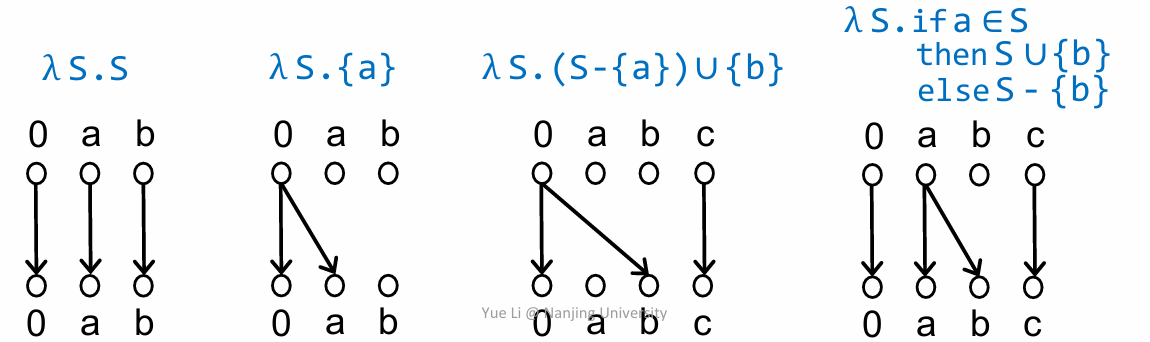
上面的这是四个例子，

• λ S.S 可以理解为输入是什么输出就原封不动的输出（没有涉及到初始化相关的语句时，就用 λ S.S 表示），所以就是三条竖线。
• λ S.{a} 可以理解为不管输入是什么，输出只有 a（b不会被输出了），那么根据前面的规则，1,2 满足条件，连线即可。
• λ S.(S-{a})∪{b} 同理，a 不会被输出，且 b 会被输出
• 第四个对应第三条规则，即 a∈S 时，b 会被输出，则相应的就会有 a 到 b 之间的一条边

如果觉得这些理解起来有些抽象，那么一定要结合我们的目的来理解，就是哪些变量没有被初始化，哪些变量被初始化了，如果被初始化了，那么其就不会存在相应的边进行连接，从而也就不会被传递（用于后面的 reachability）。

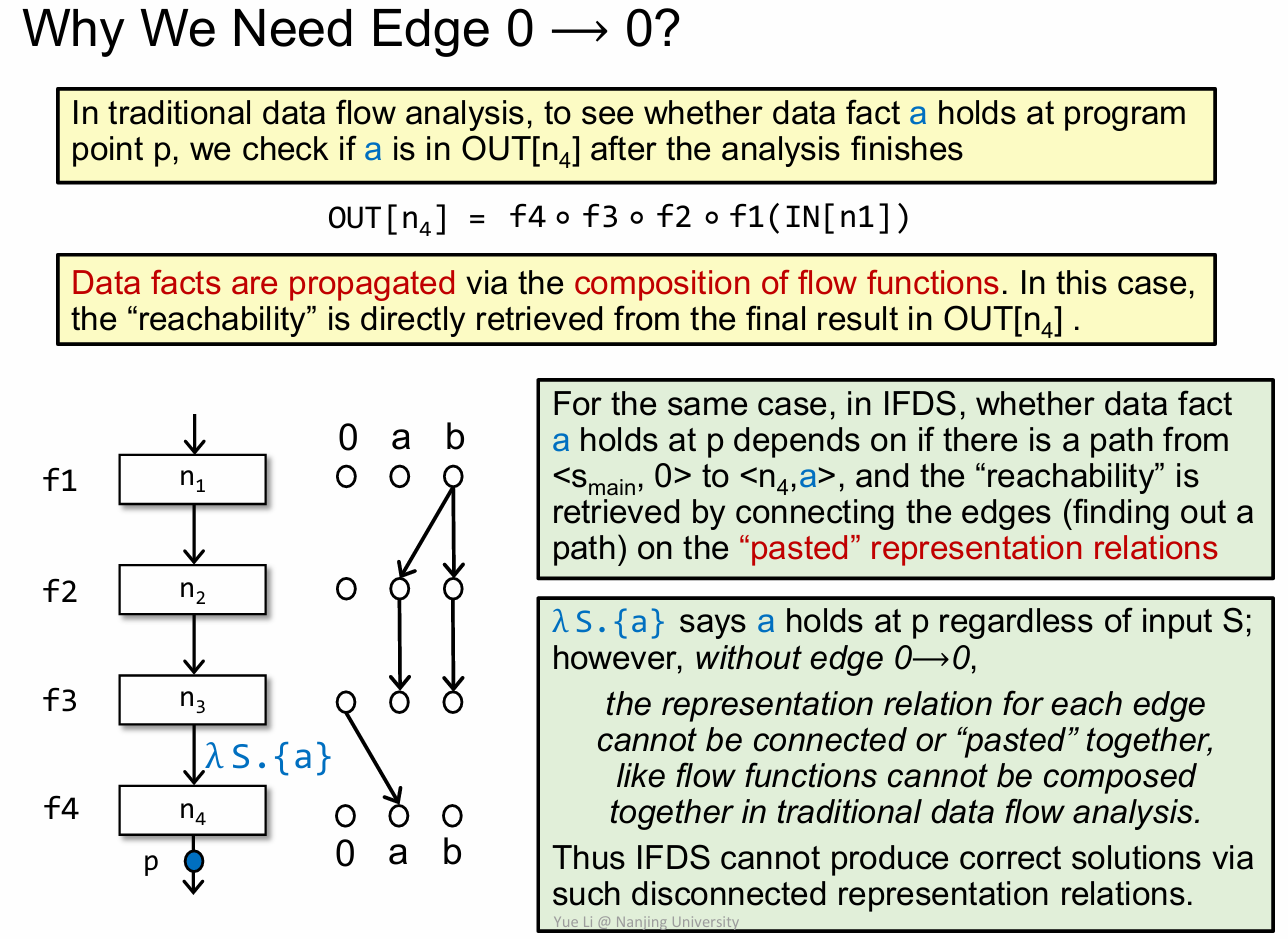
这里给出了为什么需要设置 0 到 0 的边，解释的比较详细了，不在过多说明。

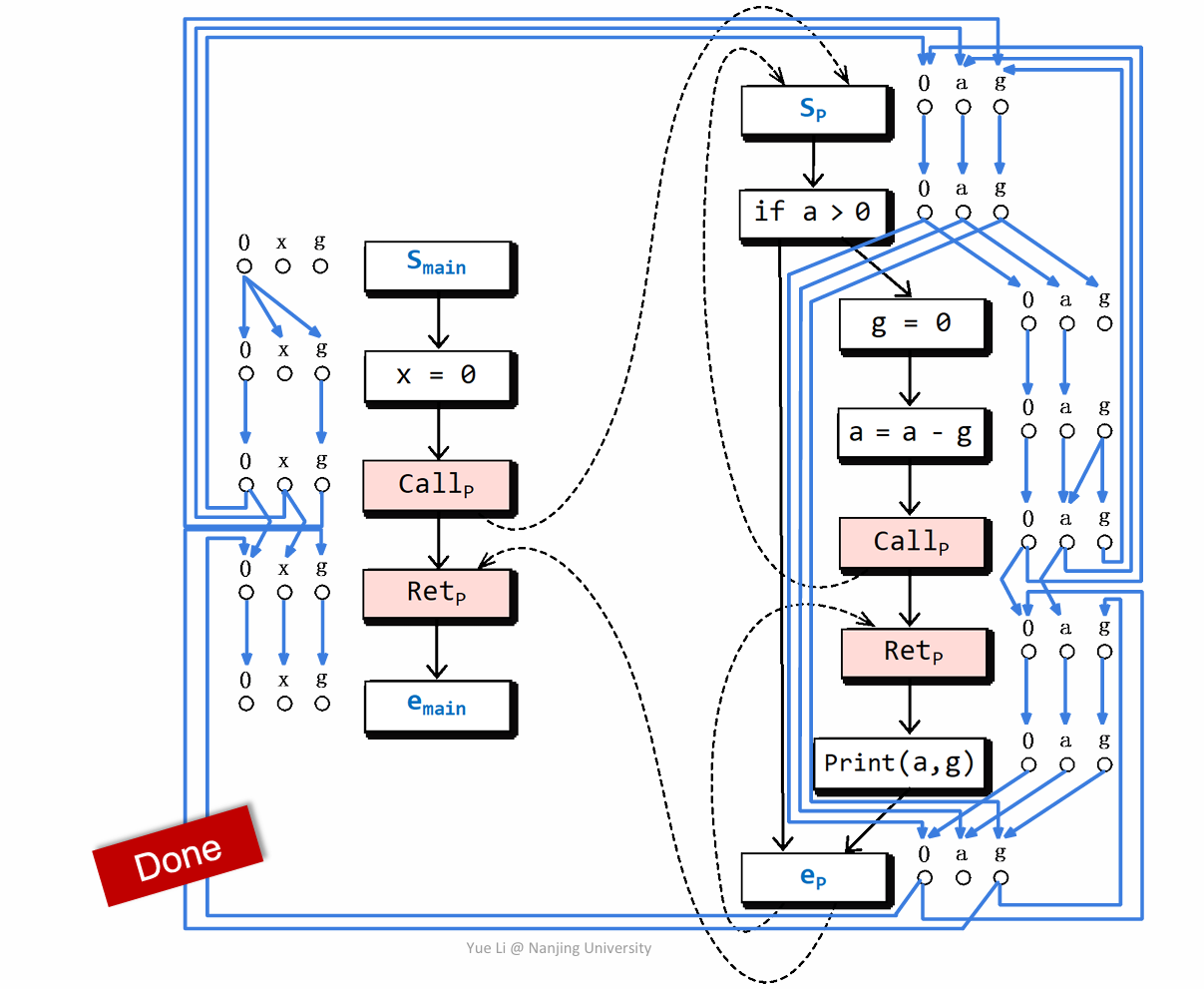
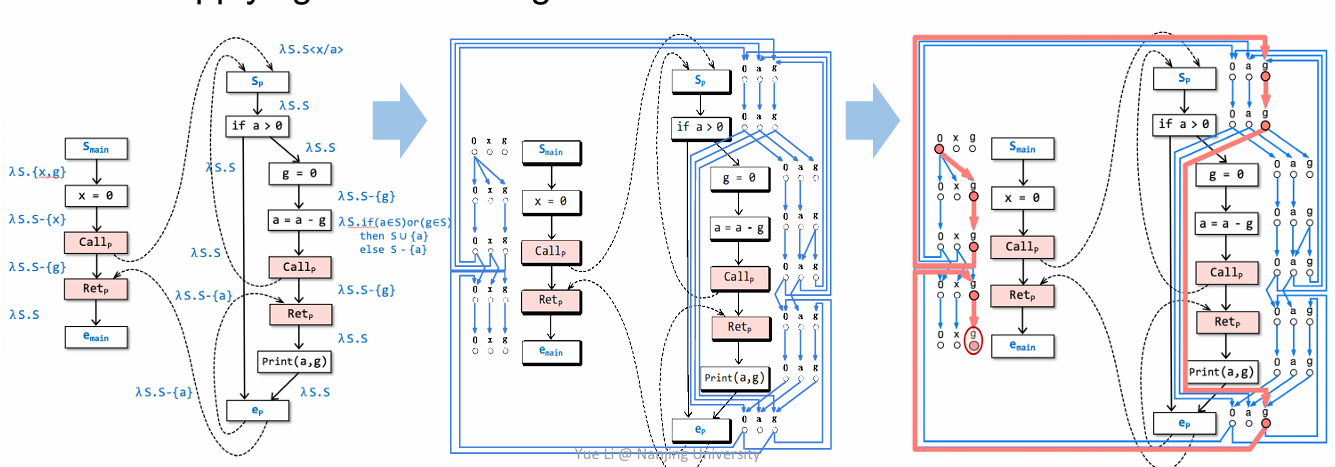
这张图就是根据流函数然后匹配 的规则，最后建立完成的 G#，乍一看比较唬人，其实分开一点一点剖析就会明白了。

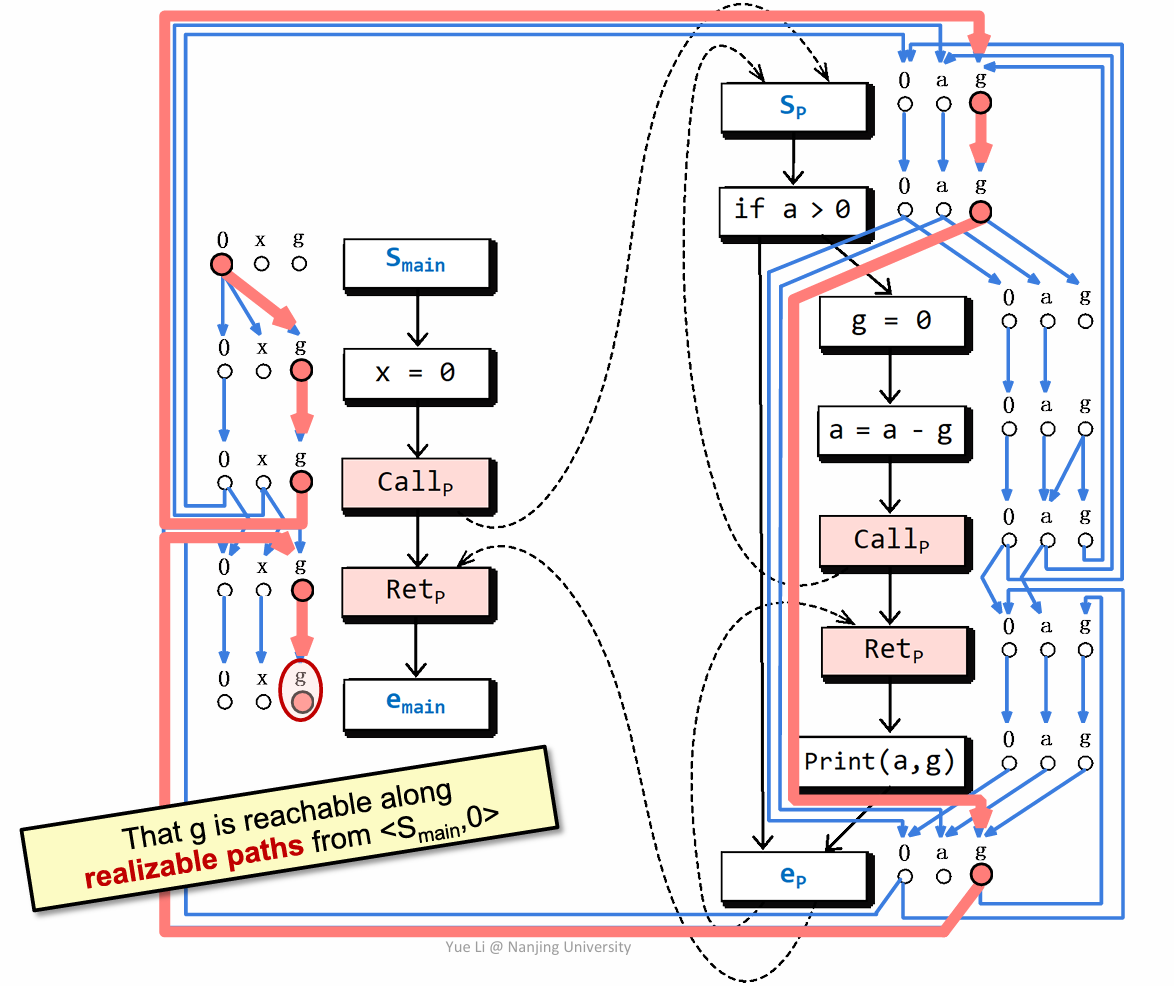
这条红色的边就是我们需要找的，即存在一条 g 不会被初始化的边。

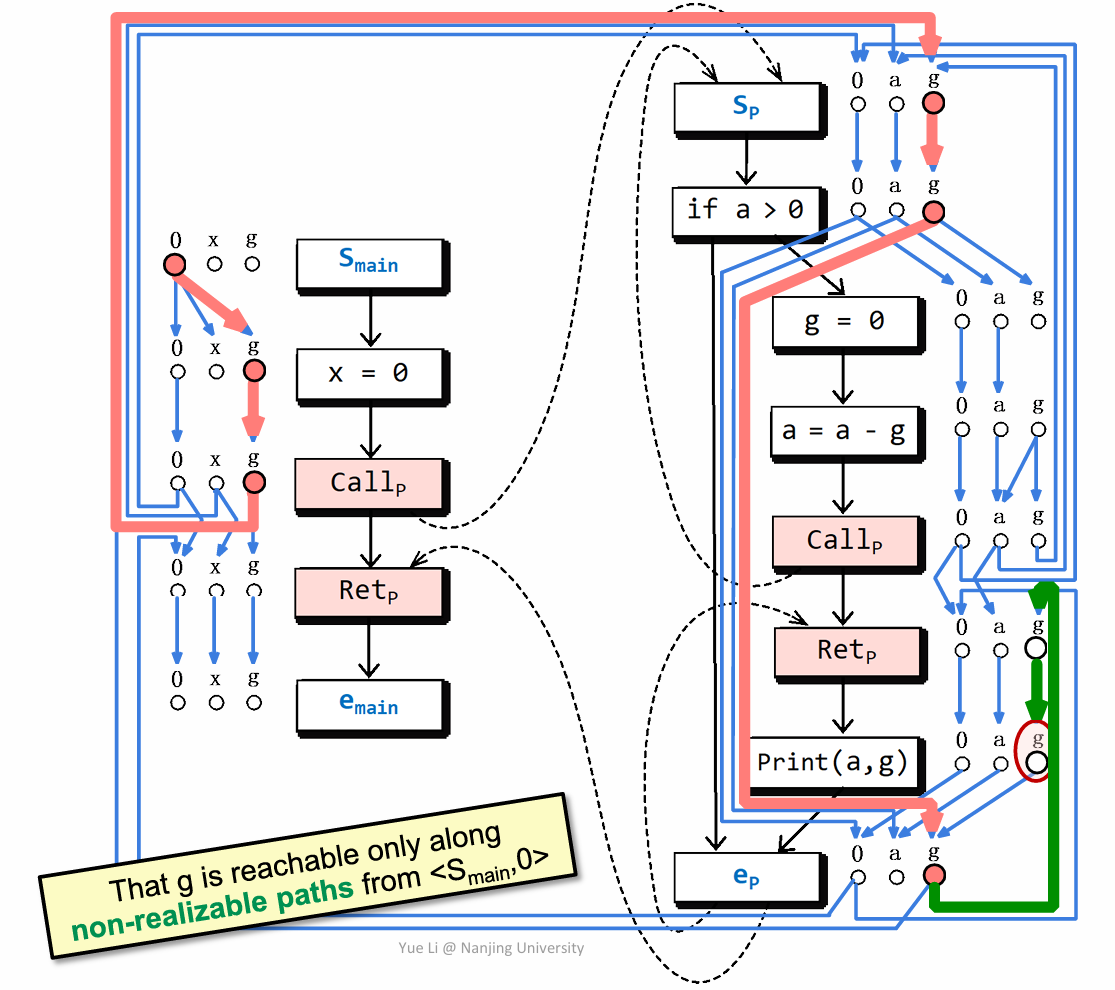
当然也可能会存在这样的边，如红色连过去之后接着绿色，那实际上这种边是不满足前面提到的 CFL 的匹配规则的，因而也就会丢掉这些没有用的边。

Tabulation Algorithm

tabulation 的完整算法如下：

由于 tabulation 算法所涉及的内容较多，所以老师这里也是只简单的讲了 tabulation 的一些核心

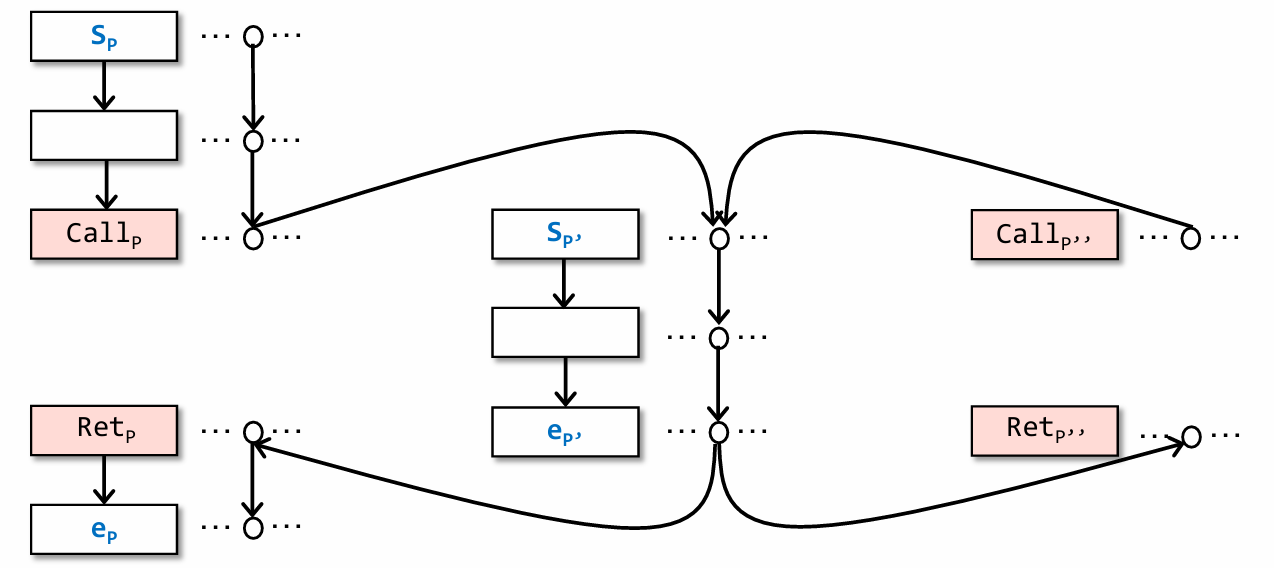
对于这样一个已经建立完成的 G#，tabulation 需要将这些 node 进行识别，需要判断这些 node 是否可到达（判断可达性是根据前面 CFL-Reachability 的知识）。

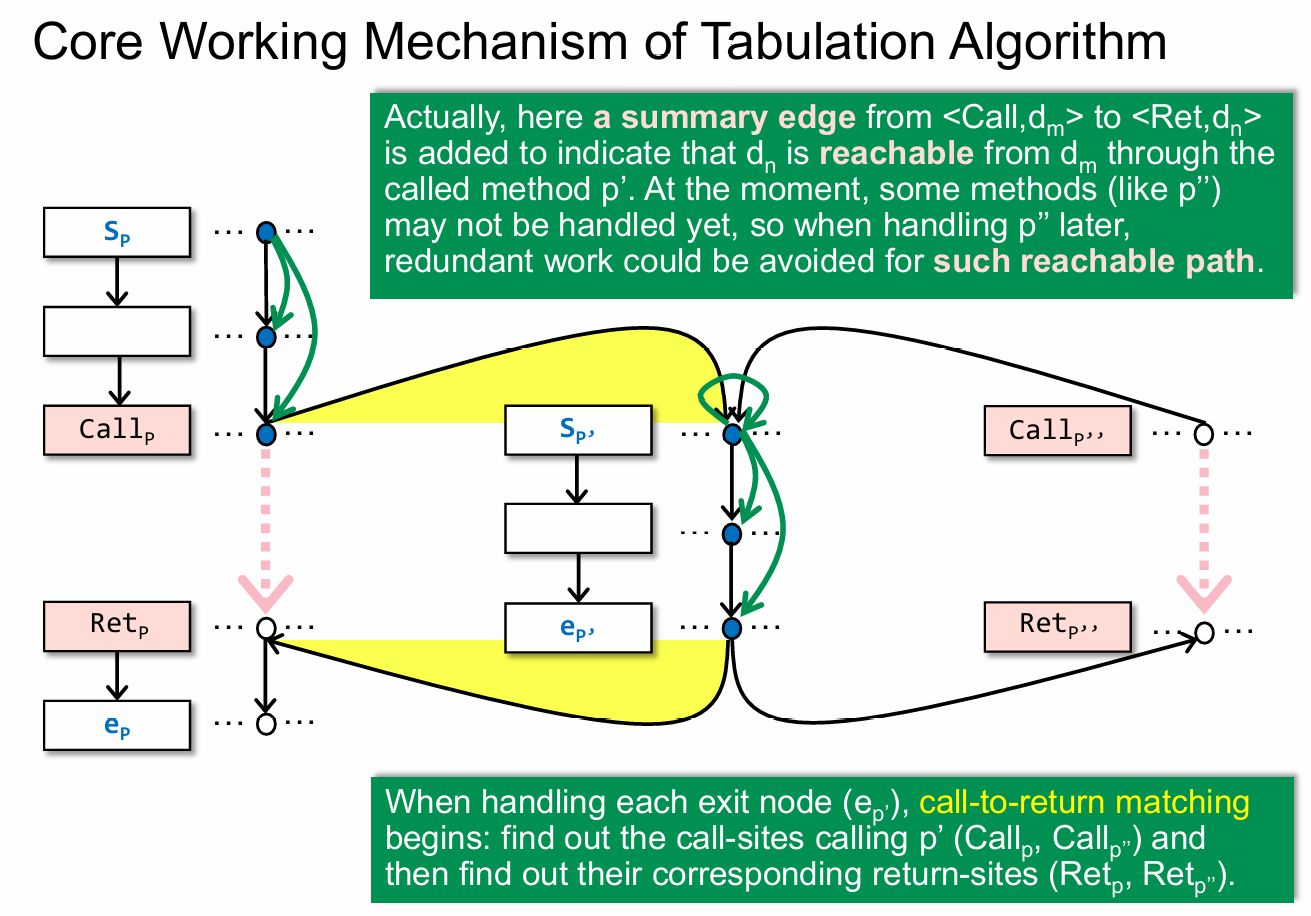
上图中蓝色的点，即代表可达的点。

Distributivity of IFDS

分配性是 IFDS 最终要的一个性质，这关乎一个问题是否可以使用 IFDS 解决。

这里直接给出结果，就是常量传播和指针分析都不能够使用 IFDS，原因是它们都不能够满足 Distributivity。

首先来看常量传播

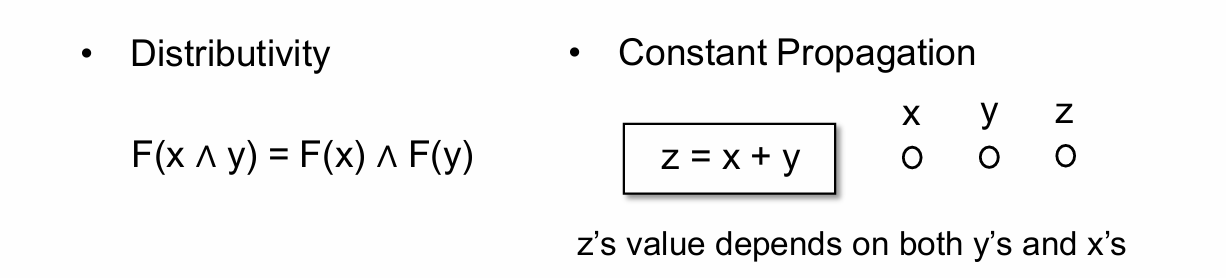
结果如下

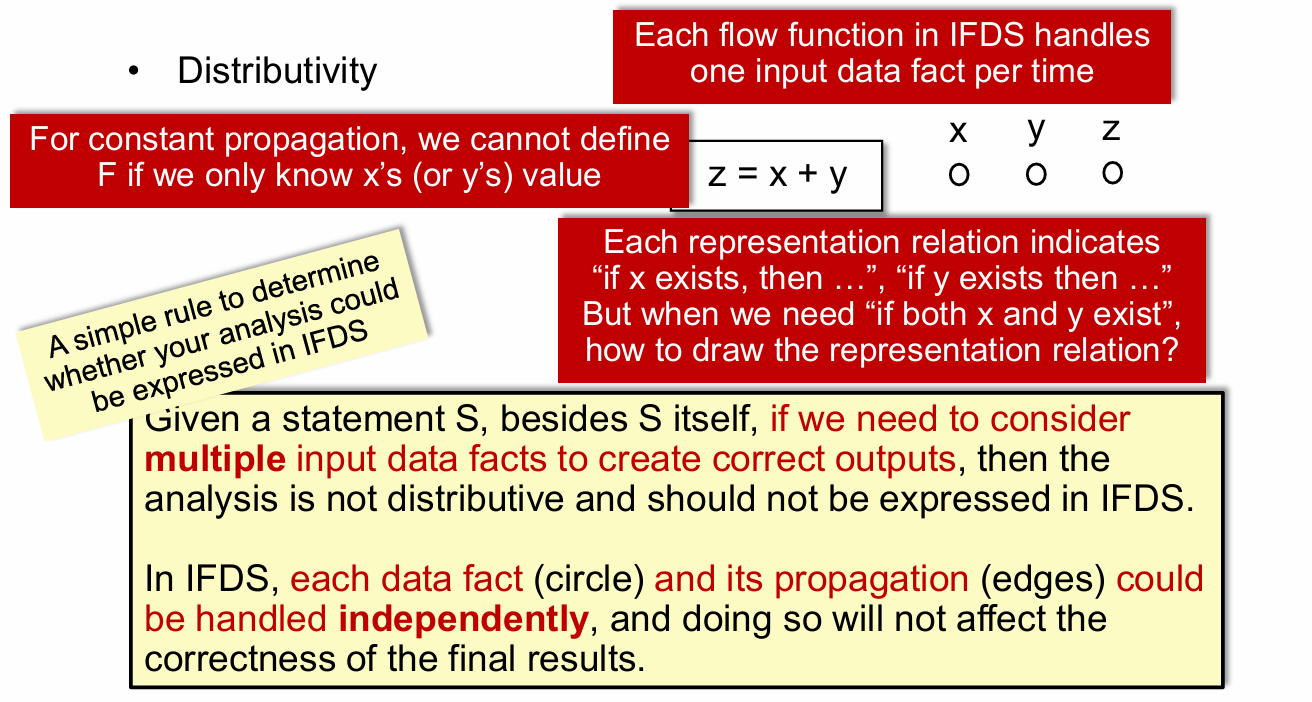
上面这些内容其实就主要说了一件事，就是 IFDS 一次只能处理一个输入的情况，当有多个输入需要同时处理时，那么它就是不 Distributivity 的，即不满足 IFDS。

同时这里也给出了一个例子来说明，对于指针分析使用 IFDS 也会得到不正确的结果，原因在于没有考虑别名分析。

总结

CFL-Reachability 这一部分理解的还不算深入

思考题