课程环境：https://tai-e.pascal-lab.net/lectures.html

课程视频：https://www.bilibili.com/video/BV1b7411K7P4

南大《软件分析》6.0 Data Flow Analysis - Foundations II

再来回想不动点理论讲了什么，就是给定一个 complete lattice，如果它是单调的，并且有限的，那么它一定存在不动点，且求出来的不动点一定是最小的。这一部分基于我们上一部分介绍的概念，并将前面的数据流分析采用的迭代算法与我们的不动点理论串联起来。

Relate Iterative Algorithm to Fixed-Point Theorem

上图左边部分显示了我们算法的迭代过程，其过程其实就可以看做是一个 product lattice 在其域内的变化过程，同时这个 lattice 自身也是有限的，如何理解这个有限呢，其实就是它的状态变量是有限的，在上图反映的就是 。

对于单调性的证明，我们需要考虑迭代算法自身，迭代算法由两部分组成，第一个是 transfer function，也就是转换规则；第二个是 join/meet 操作。

对于 transfer function 我们在之前 Reaching Definitions 中已经有过介绍，其总是单调的。其次就是 join/meet 操作是否是单调的，上图给出了关于 ⊔ 操作的单调性证明。

现在我们将迭代算法和不动点理论联系了起来，意味着我们之前所有的不动点理论都可以用在迭代算法里面，由 5.0 的知识，我们已经可以解决上图中第一和第二个问题。

关于第三个问题关注的是算法在什么时候会到达固定点，或者什么时候可以得到结果。

由前面的数据流分析的内容可以知道，每次只要有一个结点的 bit 位发生变化，就会重新执行一次迭代算法，如果不在变化，则算法终止。

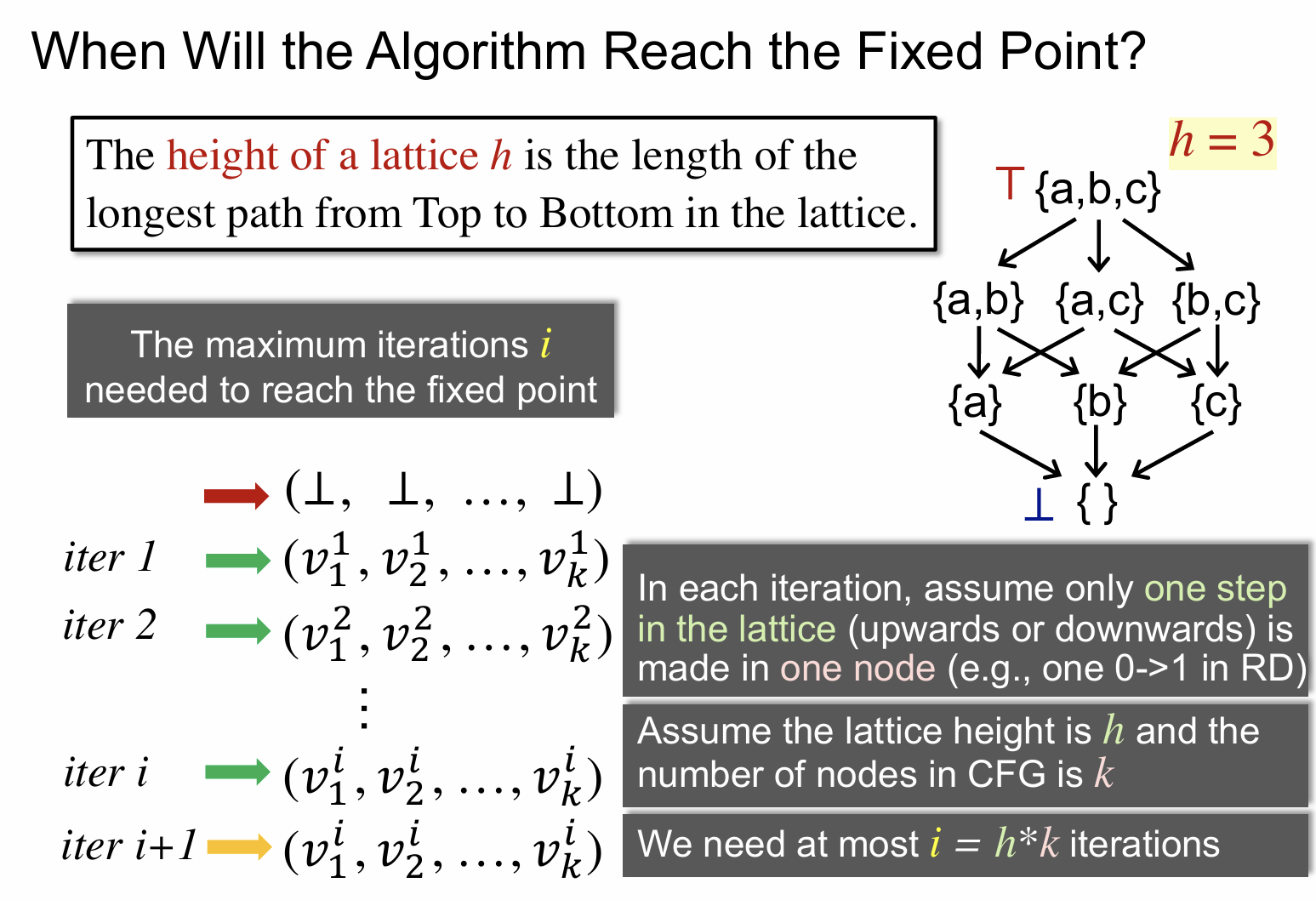
来看看上面这张图的右边部分，可以看作是一个节点的 lattice，比如说 {a} 代表 {1,0,0}；{a,c}代表 {1,0,1}。我们定义其高度为 3。左边文字也是给出了高度的定义，即从最高到最低的需要经过的最长边数。这个高度怎么来理解呢，上图是一个 complete lattice，且满足单调性和有限性，这意味着我们只要经过有限的迭代次数，势必最终会到达一个固定点，而在最坏情况下这个固定点就是最低到最高之间的最远距离，因此 lattice 的高度就是用来描述这一含义的。

假设一个 CFG 的结点个数为 k，且其高度为 h，那么就意味着最多 k*h 次迭代之后就可以得到最终结果。

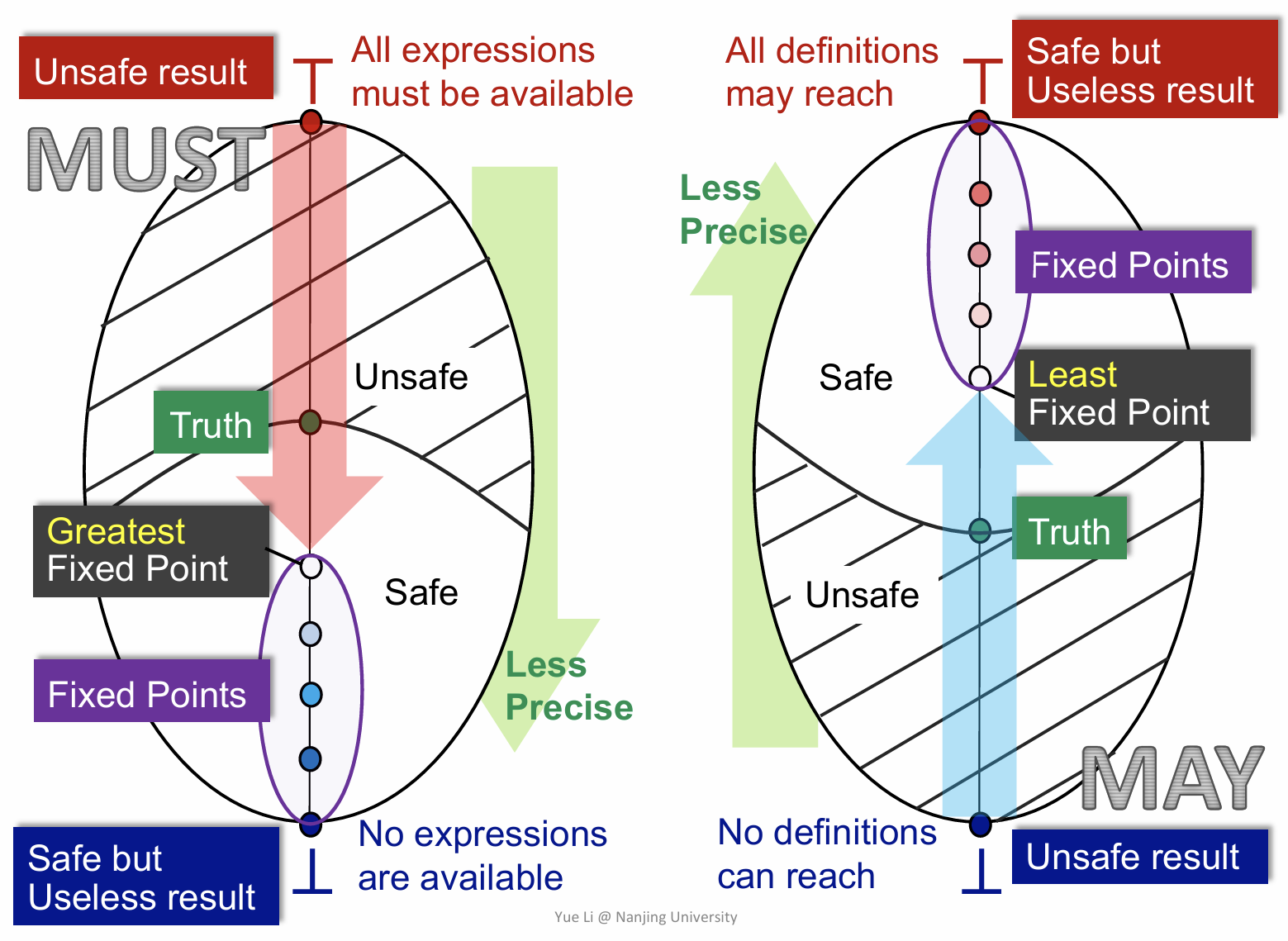
May/Must Analysis, A Lattice View

上面这张图非常非常重要，给出了一个从 lattice 的视角来看待 must 和 may analysis。需要注意的是这两者都是从 unsafe 到 safe 的一个过程，而且最终都会在各自的环境下，达到最小或最大不动点。建议把这个图里面每一个字每一个图都认真理解。

MOP

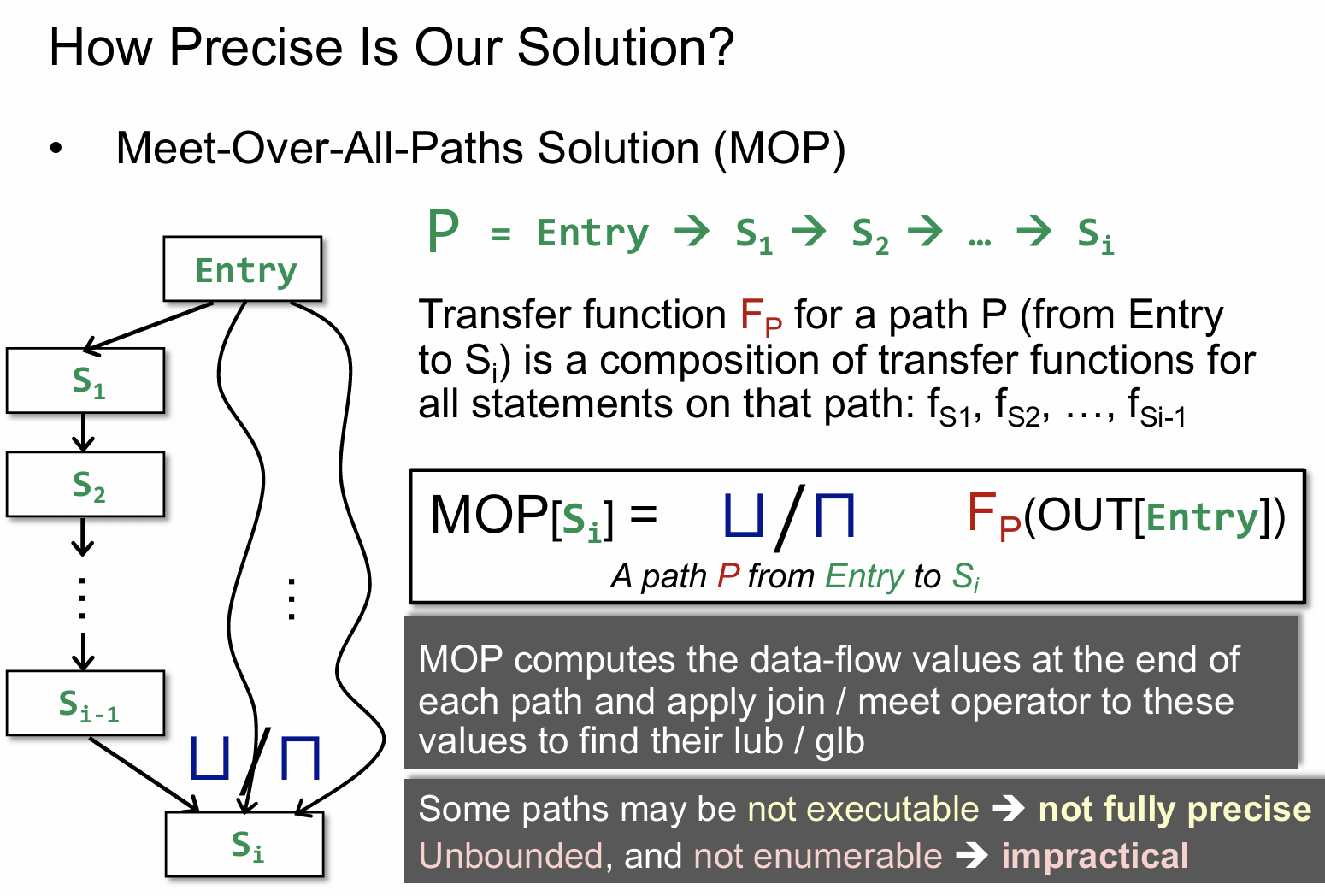
MOP 如上图所示，简单理解就是，它先关注的是每条单独路径上的状态转化，到最后把这些所有路径上的最终结果执行一个 meet 操作。

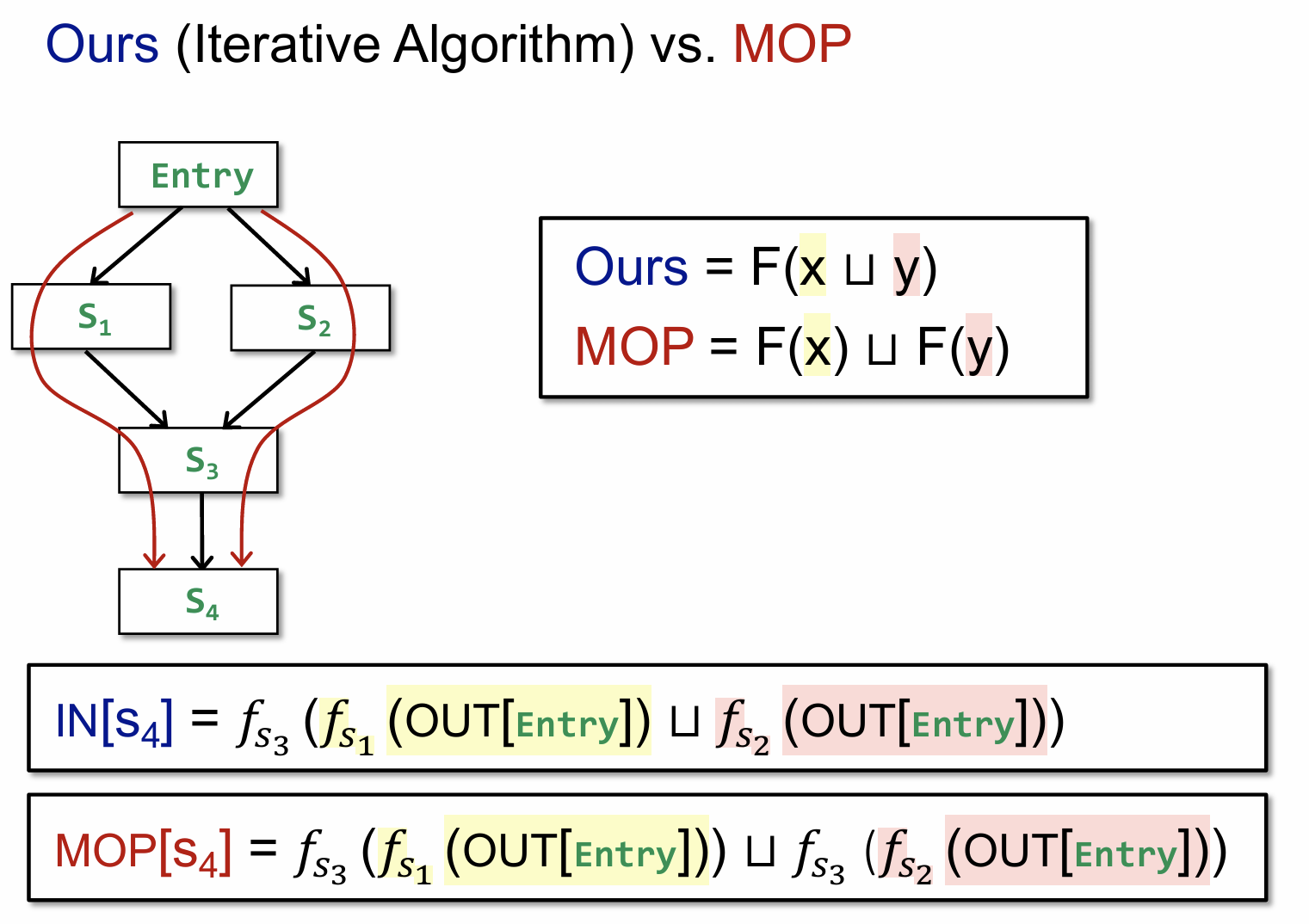
上图的 OURS 是我们之前迭代算法中计算的一种思路，即我们会关注每一个块的输入输出状态，但是 MOP 所采用的思路并不相同，它以开头和结尾作为两个端点，关注从头到尾所有可能的路径，并将每条路径的结果在最后进行一个汇总计算。

有了前面的 OURS 和 MOP 的计算方式，自然也就有了如何判别这两者之间的区别，上图证明了 MOP 的精确度是大于等于 OURS 的。当然这里也给出了，当 transfer function 满足分配性时，有MOP = Ours。

而这里有个概念如下：

Bit-vector or Gen/Kill problems (set union/intersection for join/meet) are distributive

大概意思就是说我们之前提到过的那三种数据流分析都是满足分配性的，自然而然最后的结果也满足 MOP = Ours，当然这里也没有给具体的证明，暂时略过。

Constant Propagation

当然也有一些分析是不满足分配性的，比如说 Constant Propagation，它的定义如下：

上面这段定义大概意思就是说，在程序点 P 给定一个变量 x，判断 x 是否在点 p 保证拥有一个常量值。

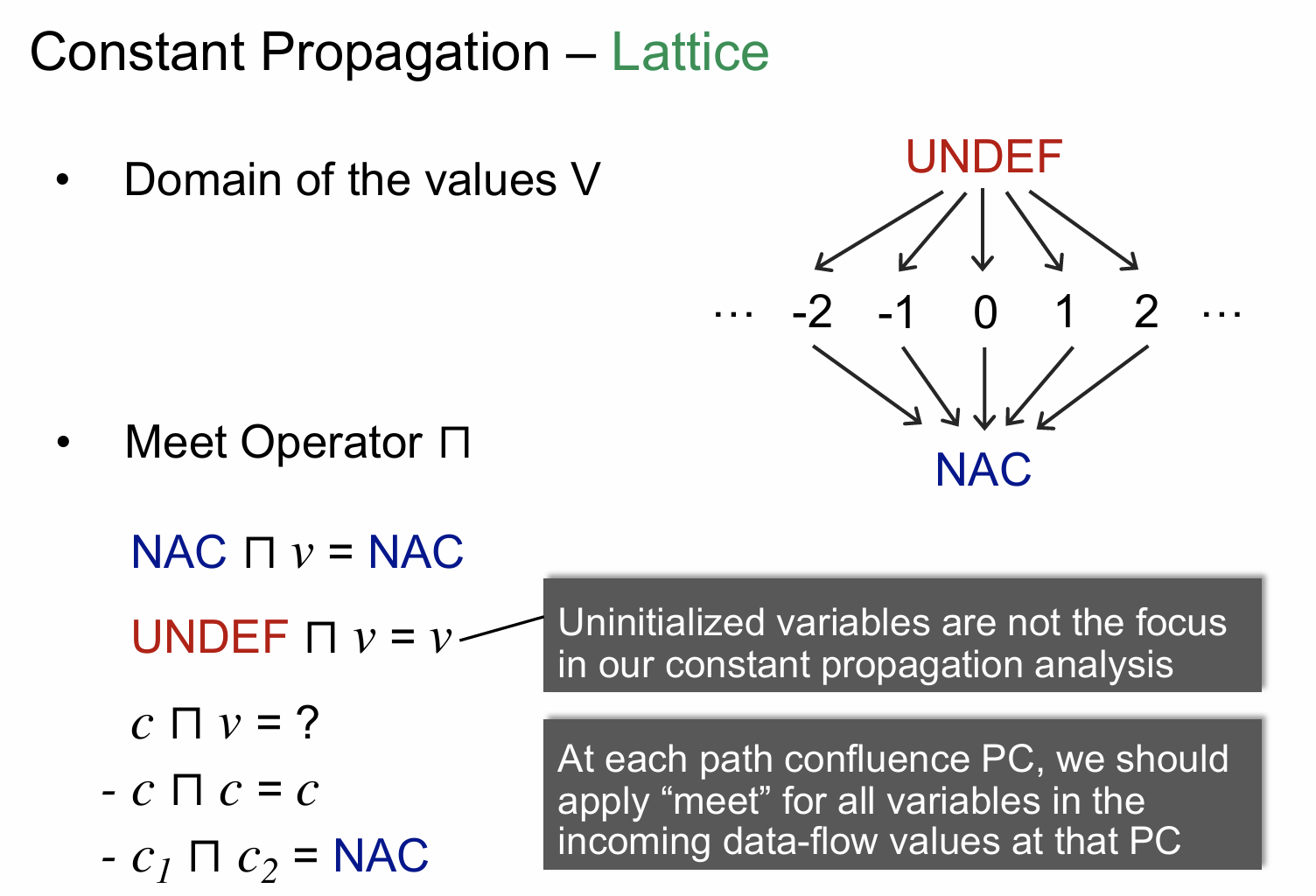
上图首先给出了常量的一个值域，其中 NAC 代表是一个非常量值，UNDEF 这里代表一个特殊的常量。需要注意的是这里的 Meet Operator，实际上它并不是我们之前理解的那种交集并集，而是代表一种操作，所以说这一点需要区分开来，上图也是定义了在不同情况下运算的结果。如果对上面的运算理解有问题，后面会有一个具体的例子来帮助理解。

下面来看看它的 transfer function 是什么样的

其内容是由类似的 (x, c) 这样的元组来完成表示的。

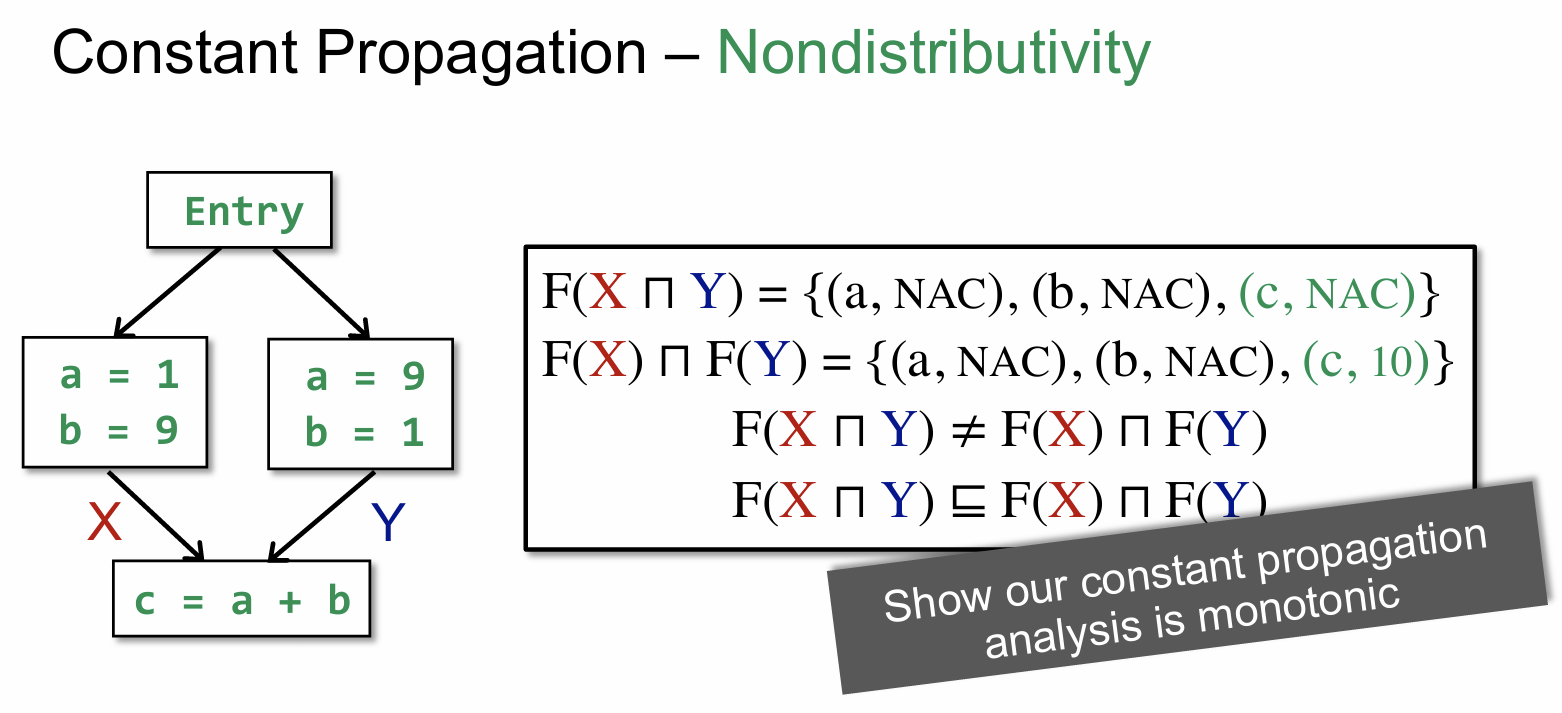
上面这张图通过计算前面提到的 OURS 和 MOP 来证明了constant propagation 不满足分配性。由于笔者第一次听到这部分时，感觉很迷，所以这里也会较详细的解释上面计算结果从何而来。

F(X ⊓ Y) = {(a, NAC), (b, NAC), (c, NAC)} 解释如下：

首先 X = {(a, 1), (b, 9)}，Y = {(a, 9), (b, 1)}，因而 X ⊓ Y 的结果为 {(a, NAC), (b, NAC)}，为什么是 NAC 呢，原因很简单，既然两条路径在到达 C 时，其变量值并不是一个固定的常量值（在这里 X 分别有可能为 1或 9两种情况），因此我们将其标记为 NAC。因此 F( X ⊓ Y ) = {(a, NAC), (b, NAC), (c, NAC)}，c 为 NAC 的理由是其由 a 和 b 计算得到，而这两个值为 NAC，其计算出来的结果 c 也必然为 NAC。

F(X) ⊓ F(Y) = {(a, NAC), (b, NAC), (c, 10)} 解释如下：

F(X) = {(a, 1), (b, 9), (c, 10)}，F(Y) = {(a, 9), (b, 1), (c, 10)}，自然而然 F(X) ⊓ F(Y) = {(a, NAC), (b, NAC), (c, 10)}。

Worklist Algorithm

该算法实际上是前面迭代算法的一个优化，前面迭代算法只要有一个结点的一个bit发生变化，就要重新对所有节点执行一次迭代算法。因此存在一定程度上的优化，优化算法如下：

其实这个优化算法也是根据 transfer function 来的，即 gen 和 kill 是固定不变的，剩下一个影响结果的因素就只有 IN 了（和 OUT 相对应） ，如果对于一个节点来说其 IN 不在发生变化，意味着其 OUT 也不会发生变化。相反如果一个节点 IN 发生变化，那么其所有后继节点的 IN 都可能发生变化，因此会将它们全部加入到 worklist 重新计算器 IN 和 OUT。

思考题

再次强调思考题里面涉及到的知识点一定要理解清楚，不然就会像我一个学废了。