南大《软件分析》5.0 Data Flow Analysis - Foundations I

这一节实际上是提出了一种形式化的东西，来方便完成对前面一些数据流分析的数学化描述，有些地方还是稍微有些抽象的，建议结合具体的例子来进行理解。

1.0 介绍

这张图给出了前面提到的三种数据流分析中采用的迭代算法的另外一种视角。即它将每一次迭代的结果全部用 (OUT[n1], OUT[n2], …, OUT[nk]) 表示，就是把那些 0101 数字的东西连在一起，并用表示这些数据集合。

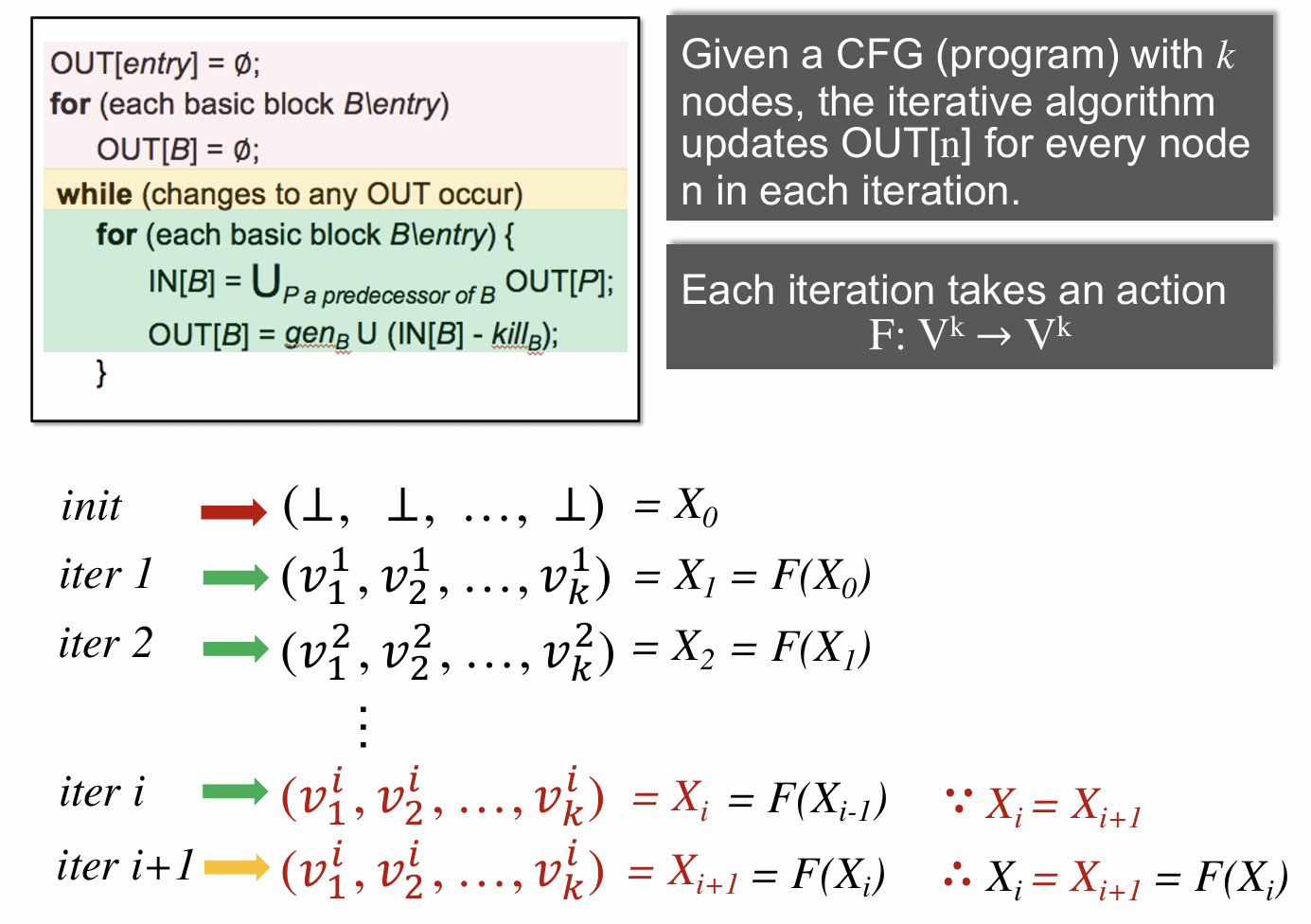
这是我们之前学过的 Reaching Difinitions Analysis 算法过程，在最后迭代的过程中，结果与上一次的一致，我们就认为是找到了一个最终的解，同时我们也可以理解为是一个不动点，即满足。

前面有说过，我们得到了一个最终解，可是不禁要问，这个算法是否能在有限时间呢迭代结束，这个解是否唯一，且这个解是否是我们所要的最优解。

后面这部分就是一些比较繁琐的数学东西（但是并不难），耐心一点还是能理解的。

首先给出了一个偏序（poset）的定义，P 可以理解为一个集合，⊑ 可以理解为是一种运算。偏序分别要满足上面的三个性质：

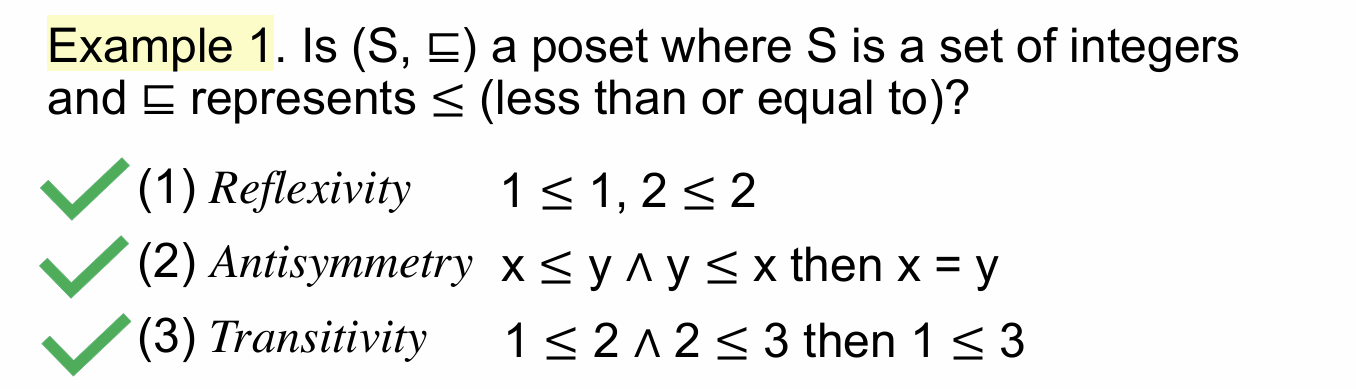
比如说上面这个例子，给定一个整数集合，且 ⊑ 表示 ≤，发现它是满足上面的三个性质的，因此 (S, ⊑) 是一个偏序（实际上这里也没有严格证明，就用几个数字带进去方便理解下，明白这个道理就行）。

上面这个例子也是一样，满足三个性质，但是我们可以发现 pin 和 sin 之间并不存在这种子集的关系，但这时候依然不影响 (S, ⊑) 是一个偏序，因为定义中并不强制要求每一对元素之间都要满足 ⊑ 的关系。

这一部分实际上就是定义了一些上下界的概念，分别如下：

分别对应了四个概念，upper bound，lower bound，least upper bound，greatest lower bound。对于这四个概念务必要认真理解，后面基本上大多数内容都是与这四个概念有关。

这里可以简单解释一下 upper bound，就是说对于一个偏序poset，存在一个 u∈P，且对于其子集S中所有的元素，都满足x ⊑ u，那么就称 u 为 S 的最大边界。lower bound 也是同理。

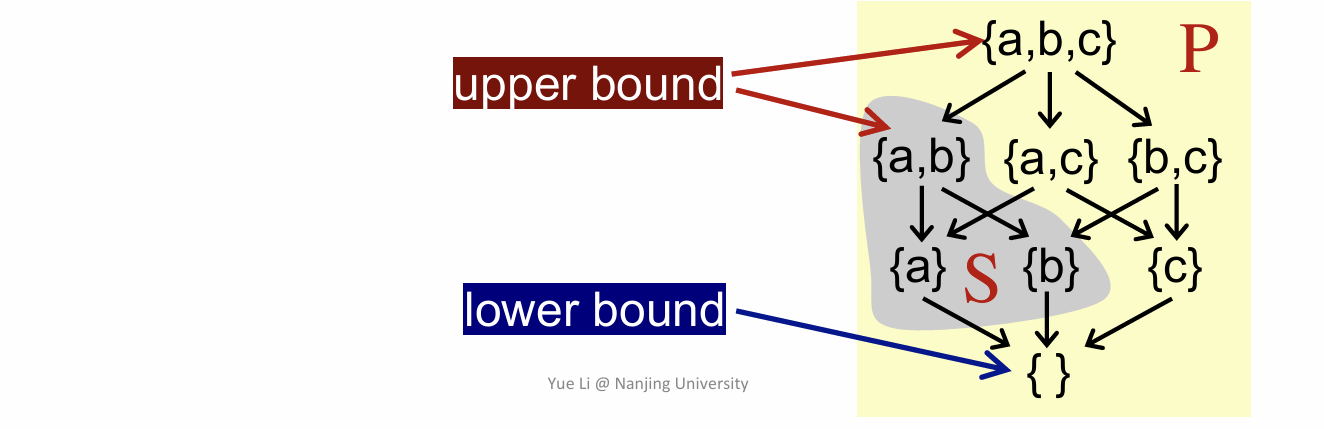
从前面的概念也可以看出 upper bound 和 lower bound 可以不唯一，只要满足条件就行，但是需要注意的是 u 和 l 一定是在 P 之内的。

least upper bound：其实就是所有 upper bound 里面最小的值。

greatest lower bound：同理，所有 lower bound 里面最大的值。

注意事项：前面图片里面的一些数学符号也建议记住，后面多用符号来表示

上图也是一种符号的情况。

需要理解的是，并不是所有的 poset 都有 glb（greatest lower bound）存在的，如上图所示，但如果一个 poset 有 lub 和 glb 那它一定是唯一的，可以用定义来证明。

Lattice（格）的概念是建立在 poset 的基础之上的，简而言之就是当一个 poset 中的任意两个元素 a，b，如果对应的这两个元素的最小最大上界（lub）和最大最小下界（glb）都存在，则称其为一个 Lattice。Lattice 关注的核心在于元素对之间的比较。

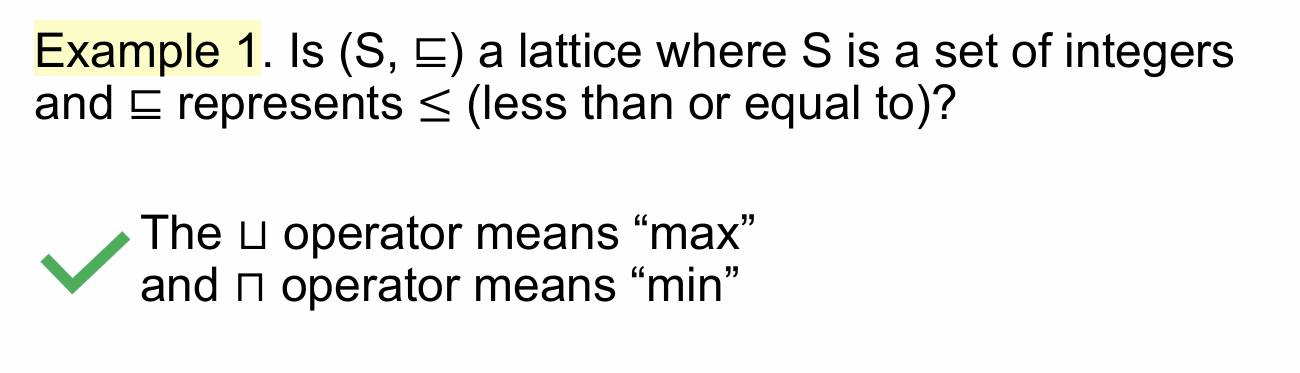
在上面这个例子中，比如说有 5,7 两个数，其 lub = 7（并操作），其 glb = 5（交操作）

这个例子前面有提到过，之前我们说它是一个 poset，可是在这里它并不是一个 Lattice，原因在于 Lattice 要求任意两个元素之间都存在 lub 和 glb，显然上面的 pin 和 sin 在图中并不在一个 lub 包含它俩。

但是这张图中，我们可以到找到，任意两个元素对都是在图中可以找到 lub 和 glb 的。

如果说前面的 lattice 研究的是两个元素对之间的关系，那么 complete lattice 就是研究两个元素子集之间的关系。借助上面 Lattice 的定义来理解。

那上面这种之前举过得例子肯定就不是一个 complete lattice，原因在于前面只是元素之间的比较，那一旦有了集合，其元素有可能就是无限的，那么就可能存在两个元素子集并不存在 lub 或这 glb。

但对于这个图来说，还是仍然满足 complete lattice 的条件。

上图的两个定义也是需要掌握的，比如说 T = ⊔P，代表的是整个 complete lattice 的 top，同理 ⊥ = ⊓P bottom 也是。

这一部分相当于是将前面的东西又进行了一次整合，一切都是为了后面的数据流分析做形式化验证准备，x 和 y 可以分别理解为一次迭代过程的输入和输出。

这里又从 lattice 的角度来给出了数据流分析的框架，具体表现为三个方面，同时也是我们前面在数据流分析方法中提到的三个非常重要的内容。

这时候就可以对前面一些提出来的问题进行回答了。

第一个问题算法能否保证终止或者达到固定点或者总是有一个解？

由于算法的单调性，可以保证上面的内容。

第二个问题是否有多个固定点（对应的解），我们求出来的解是否是最优解？

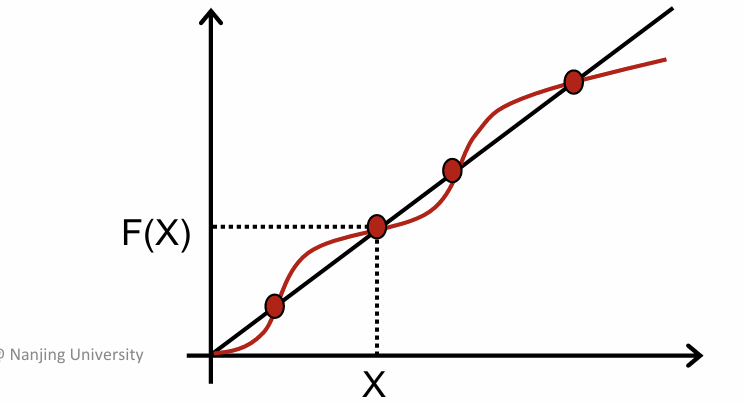
根据不动点的定义，我们发现不动点其实并不唯一。

上图给出了单调性的描述，很容易理解，但下面的不动点理论，理解起来还是稍微有点抽象的，证明不动点的存在性如下：

需要理解的是对于一个 lattice 来说 ⊥ 表示它的最小边界，而基于转换规则计算出来的 f(⊥)，也一定是在这个 lattice 的范围之内的，所以说根据定义就有了第二行⊥⊑f(⊥)的内容。

证明最后的结果是最小固定点的证明：

虽然说这一部分老师不要求强制掌握，但是理解了这些证明过程实际上是有助于后面的数据流分析的。

有点累，歇了