课程环境：https://tai-e.pascal-lab.net/lectures.html

课程视频：https://www.bilibili.com/video/BV1b7411K7P4

南大《软件分析》3.0 Data Flow Analysis

由于这一部分我个人认为如果只看这里的笔记的话可能较难理解，因为我只会写一些重点，但因此也可能会让大家不明所以。

标题提到了数据流分析，那这里肯定要提一下什么是数据流分析，它要做什么，以及它是建立在什么之上来做的。

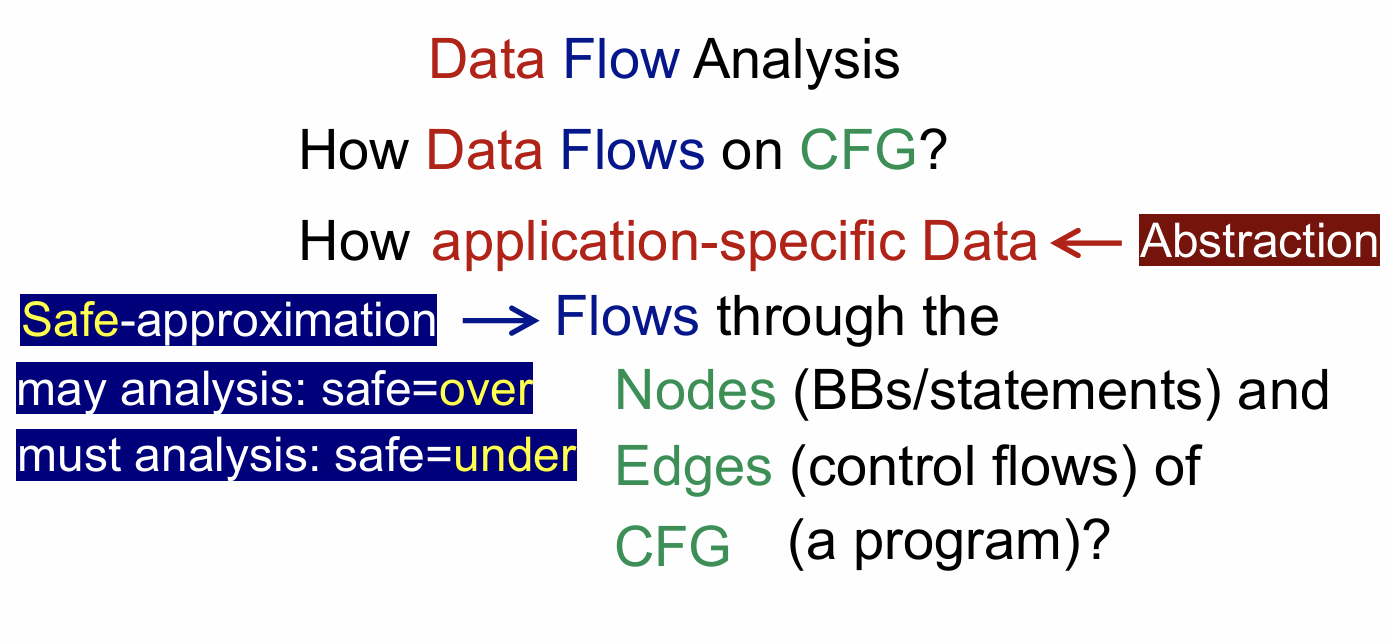
上面这张图给出了答案，

第一它要研究的是，特定程序数据是怎么在CFG上流动的

第二它是建立在程序控制流图（CFG）的基础之上，具体包括CFG的节点和边。

其中对于 must analysis 和 may analysis 的概念一定要理解清楚，可以对应第一部分 Introduction 中的 sound 和 complete 来理解，静态分析方法一般要么做 may analysis（大多数情况），要么做 must analysis，两种都有特定情况下的需求，且它们都可以说是 safety analysis。

这里有几个关键概念需要理解，就是上图中其实标有颜色的部分都指一些具体的情况（后面会有例子帮助理解）：

• Abstraction：即你要对程序如何进行抽象
• safe-appromixmation：这里面包含两种方式 may analysis 和 must analysis
• Nodes：可以在这里定义 transfer function，即转换规则
• Edges：Control flow handling 这里牵扯到对CFG中的一些边定义处理规则

明白下面的内容，可以更好帮助理解，简单来说这些东西并不固定，是可以人为根据需求来定义的。

Preliminaries of Data Flow Analysis

在数据流分析当中，有些内容是统一规定好的，其实这一部分就是定义一些符号，方便后面的各种分析方法的表示，比如说程序（单个命令或者一个基本块）的输入输出状态，这个其实比较好理解，输入状态在经过执行之后总会有一个对应的输出状态（即使这两个状态可能相同）。

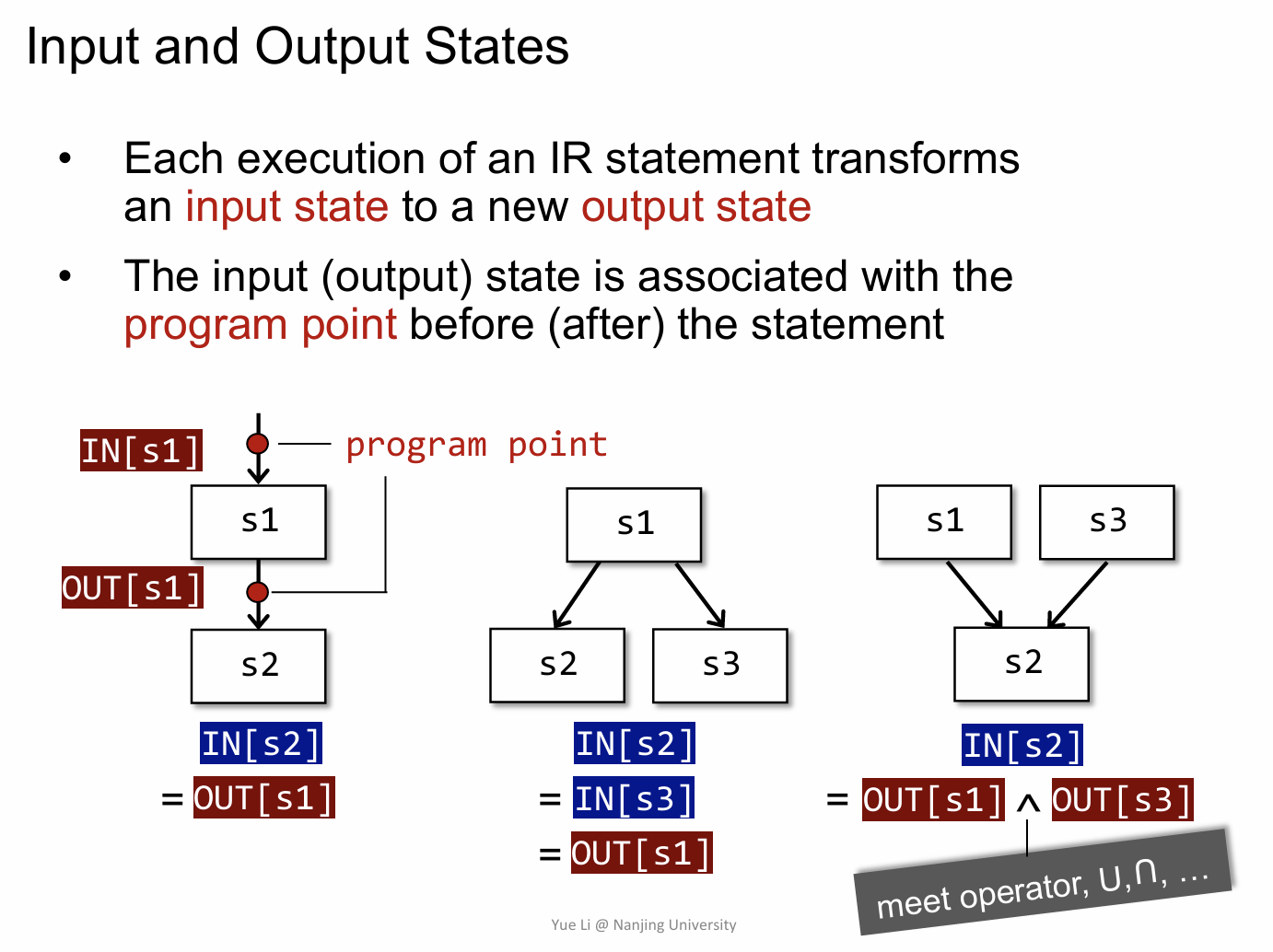
Transfer Function 的约束规则如下：

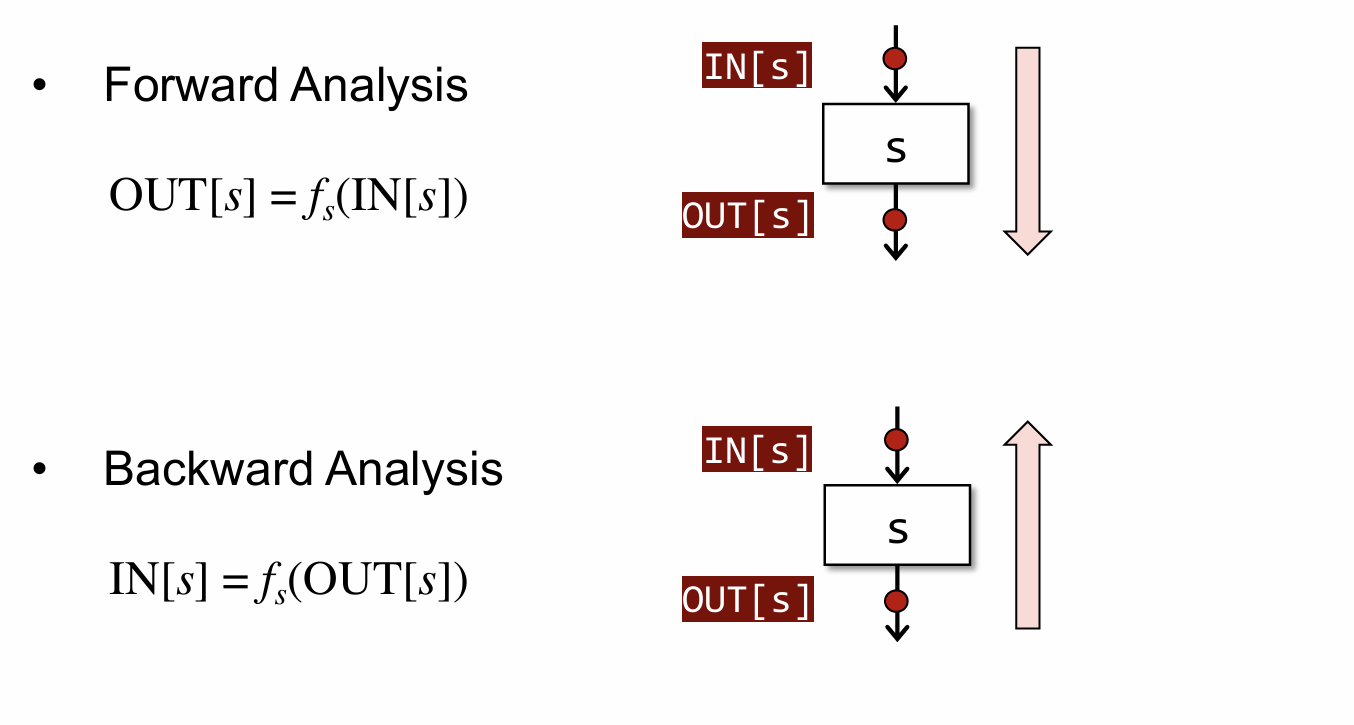
Control Flow 的约束规则如下：

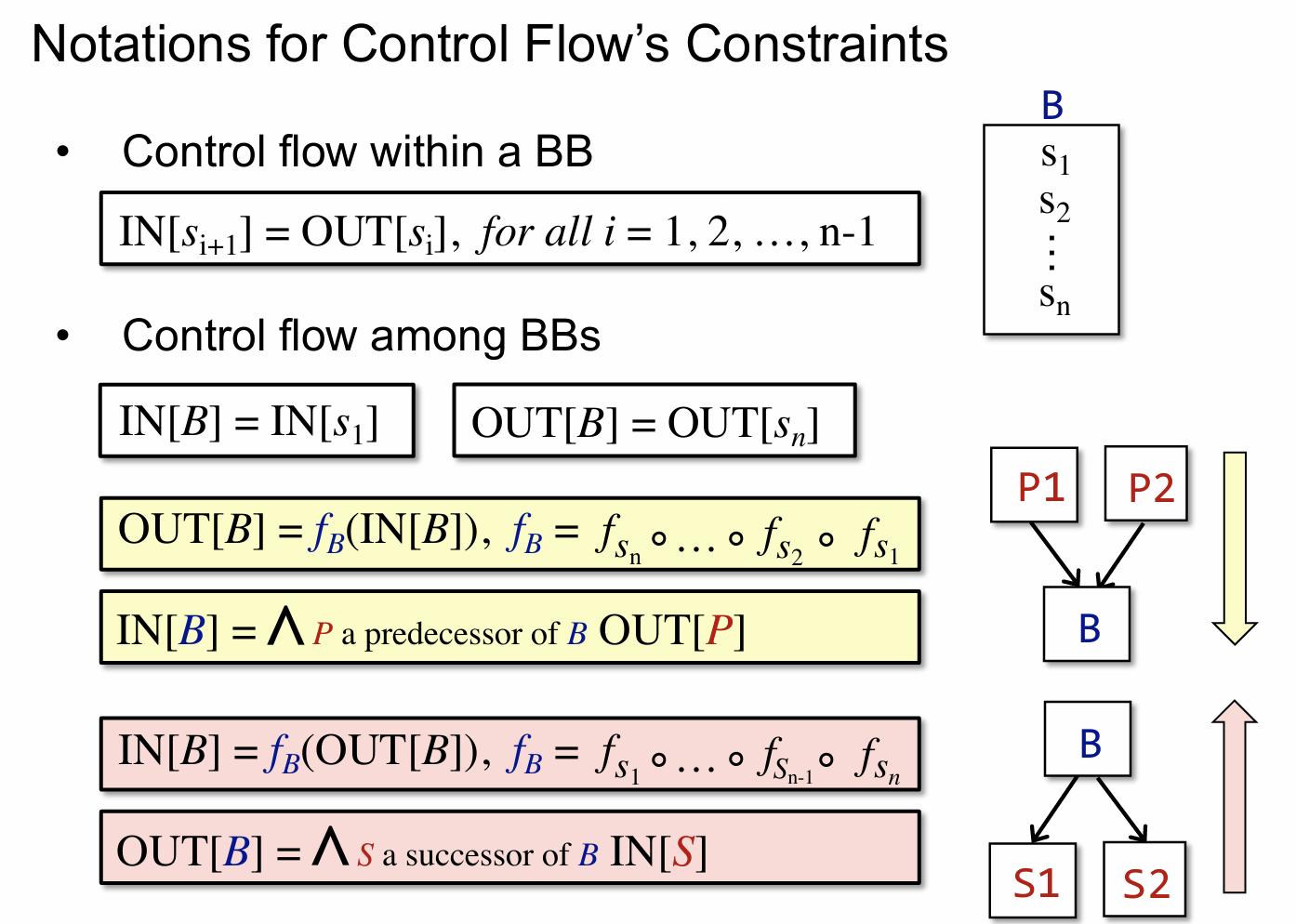
理解上面的两个约束规则是重要的，后面的分析都建立在这两个基础之上。

Reaching Definitions Analysis

这一部分就正式开始介绍第一个数据流分析方法 Reaching Definitions Analysis，注意这里不会引入 Method calls 和 Aliases，后期会介绍（老师说这里提前引入比较影响理解）。

上图给出了 Reaching Definitions 的定义，其实单看这个定义是非常抽象的（简直不是人话）。

重要部分：按照我的理解就是（已上图中下方的路径来进行说明），你在程序状态点 p 处定义（definition）了一个变量 v，ok，这里是重点，假如存在一条执行路径使得 p 可以到达 q 点，且这个过程中 v 没有被重新定义（意思就是没有被重新赋值），那么我们就说状态点 p 处的定义（definition）可以到达状态点 q。

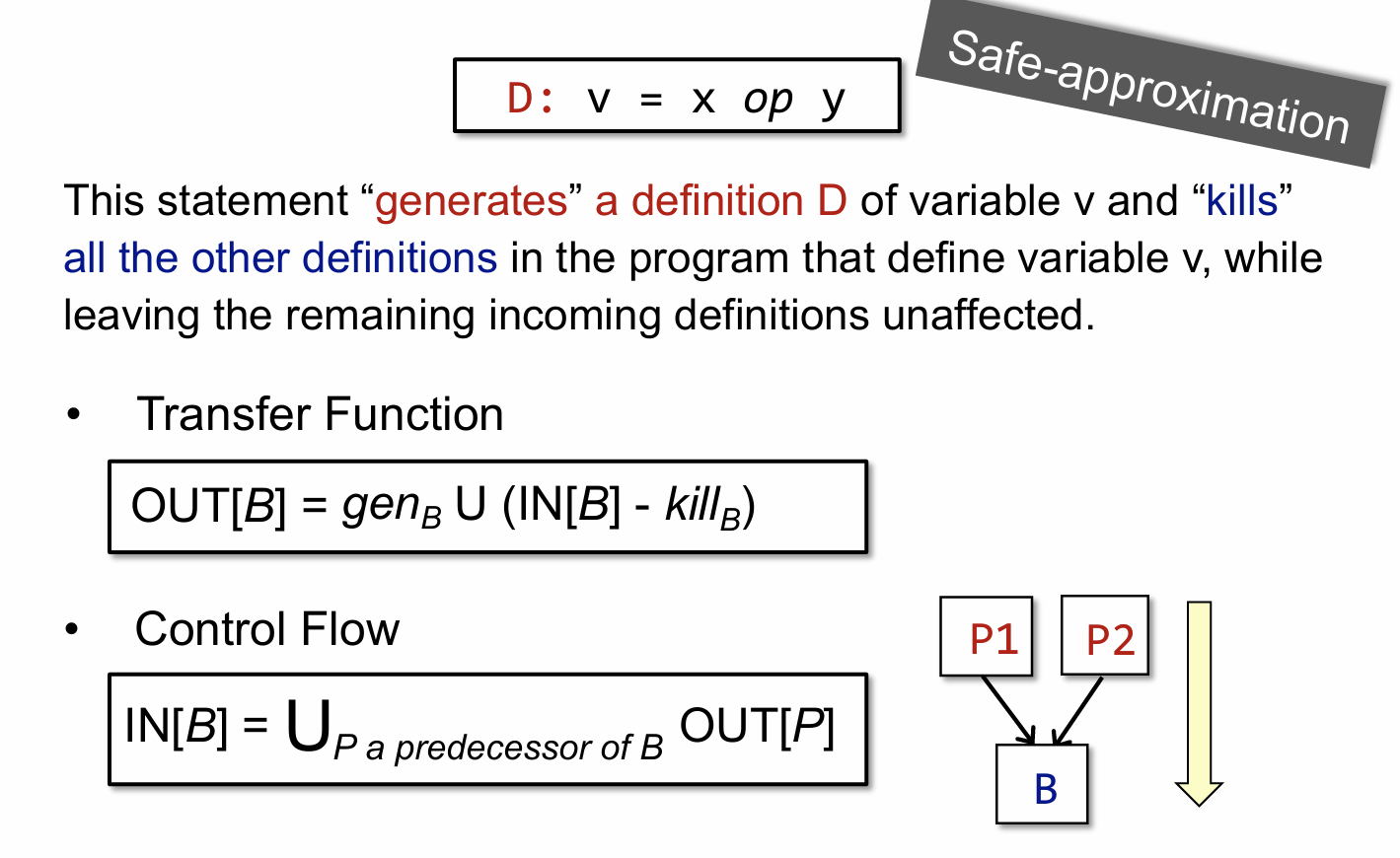
文章开头有提到，不同的分析方法，可能对应不同的 Abstraction，Transfer Fcuntion，Control Flow，包括 Safe-approximation，上图即对应的是 Reaching Definition 对这些概念的定义，注意上面的两个公式。

关于 gen 和 kill 的内容可以结合下面这张图来具体分析：

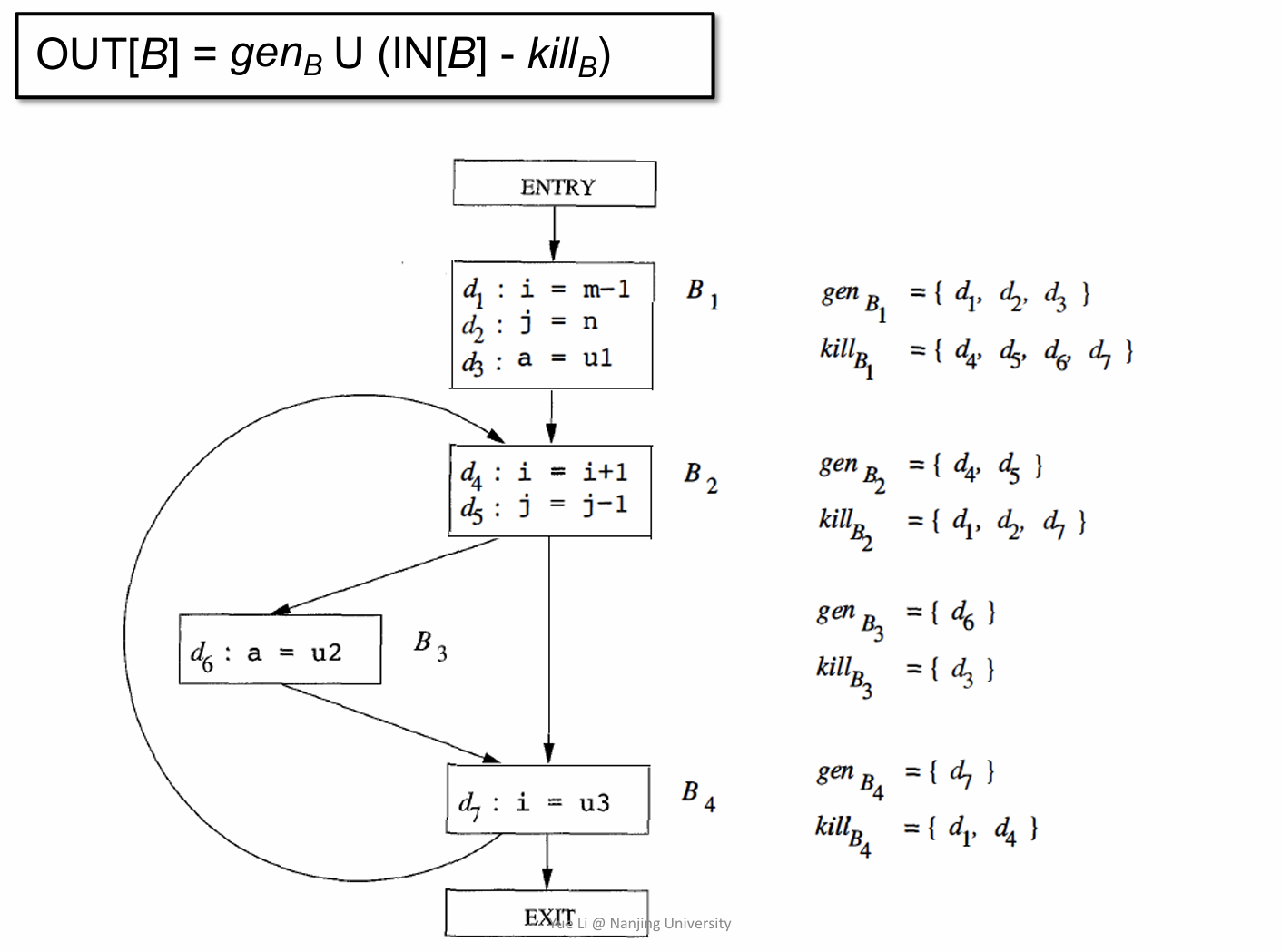
现在就是重点部分了，即 Reaching Definitions Analysis 的具体算法：

这里逐行进行解释：

• 第一行：2.0 IR 部分有提到，程序的CFG会设置一个entry和exit基本块，由于entry没有IR所以输出自然也是空集
• 第二行，第三行：对除了 entry 之外的所有基本块的输出进行初始化，且内容全部设置为空集
• 第四行：进入到一个 while 循环，循环终止条件设置为不在有 out 发生改变（是一个迭代过程）
• 第五行：只要前面有一个基本块的 out 发生变化，就会进入到这个 for 循环语句，循环的对象是除了 entry 块之外的所有基本块。
• 第六行和第七行：这部分其实前面已经提到过，分别对应 Control Flow 和 Transfer Function 的转换规则。

当然仅仅是这样，依然还有可能不明白，再来结合一个具体的例子来进行理解。

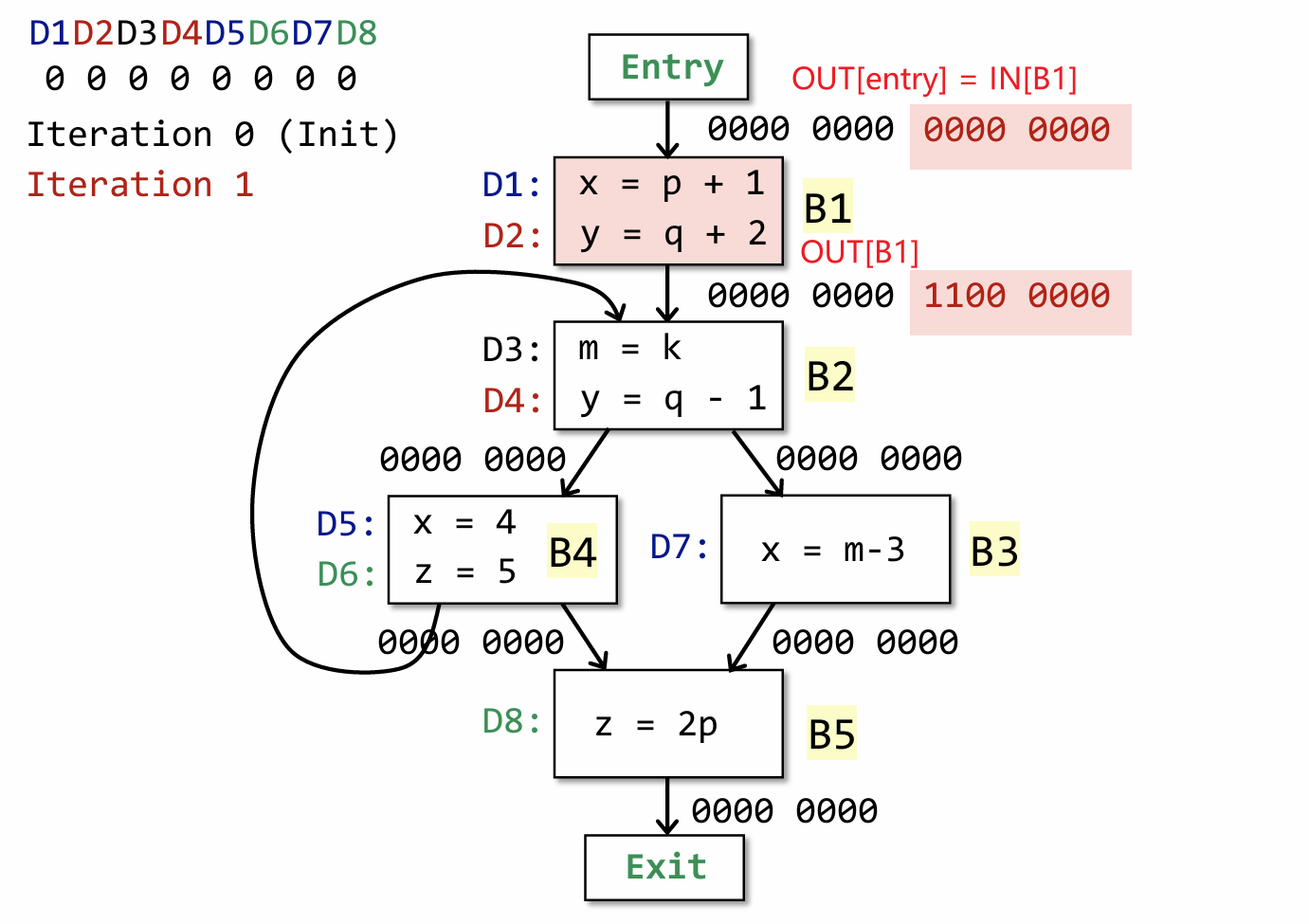
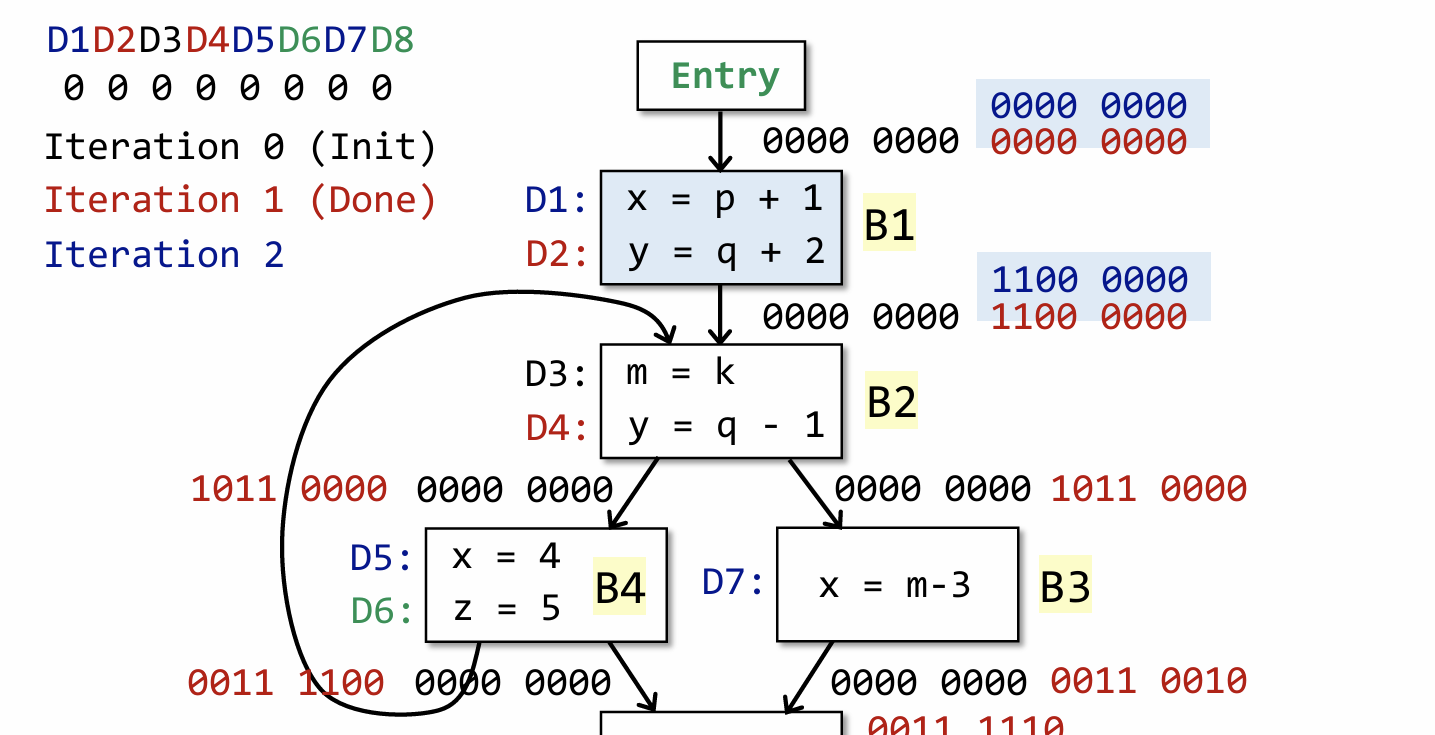
先来解释下这张图的构成，原CFG中总共有8个定义（可以理解为总共有8次为变量重新赋值），并为每一次定义都以一个符号表示，比如说上图中的 D1 和 D2，图中左上角也分别给出了这8个定义所对应的 bit 位，根据前面的算法，我们知道 OUT[Entry] 和 OUT[B1] 一开始均被初始化为 全0（黑色数字）。

IN[B1] = 0000 0000，且B1的 gen = {D1, D2}，kill = {D5, D7, D4}，由于D5和D7处x均被重新定义，所以要

kill 掉，D4 处y被重新定义，也要 kill 掉。所以根据前面计算 OUT[B] 的公式，gen = 1100 0000，

kill = 0001 1010，由于 IN[B] 为0，所以最后 OUT[B] = 1100 0000。

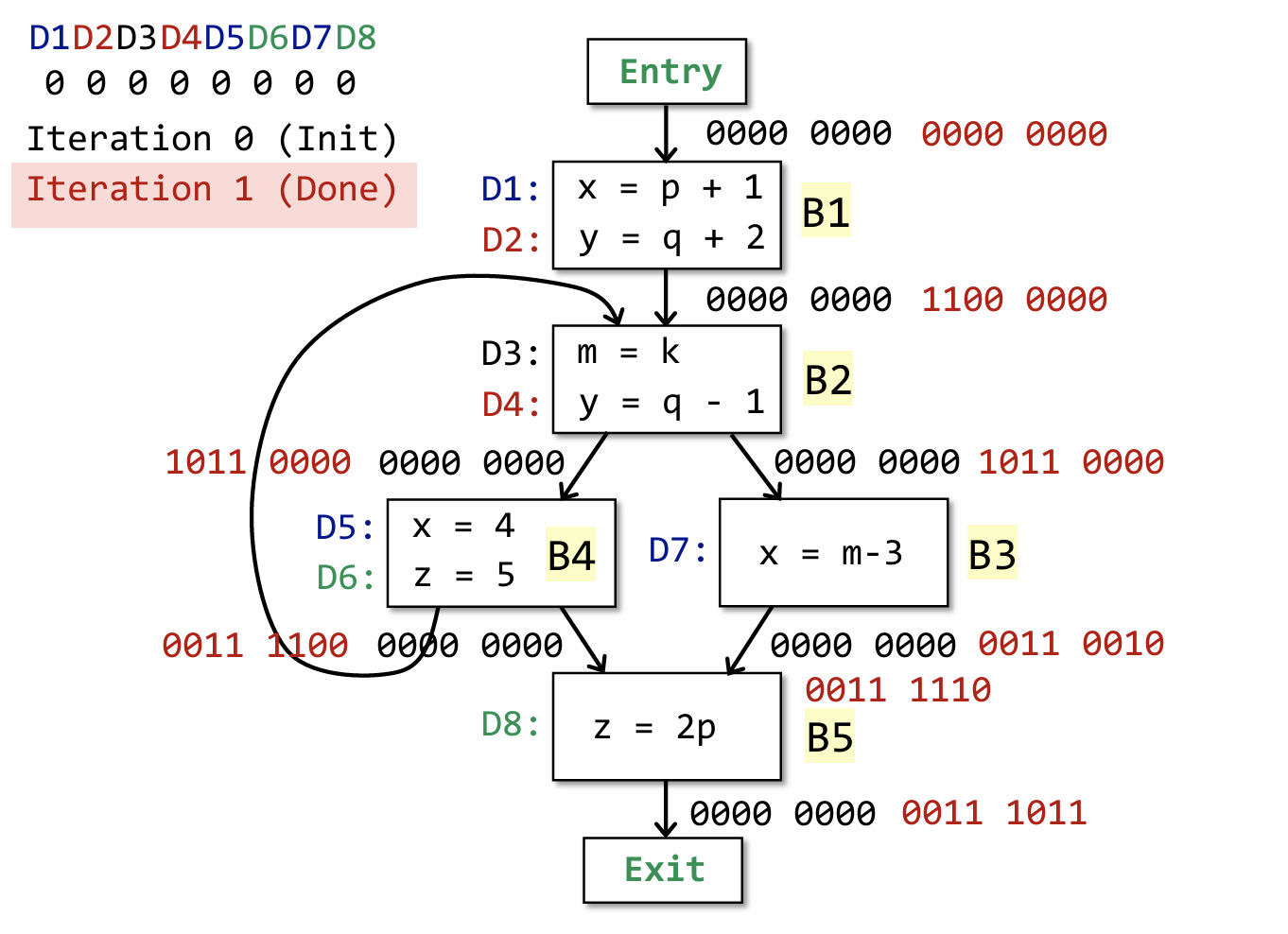
大家可以尝试着自己算一遍（这里面其实有很多细节需要注意），最后一次迭代过程结束之后，最终结果如上图所示，由于所有基本块（不包括entry）的输出都变为了非零，所以自然而然会再次进入 while 循环，然后在从头开始根据上一次的输出，来重新计算 OUT[B]，这就是迭代的过程。

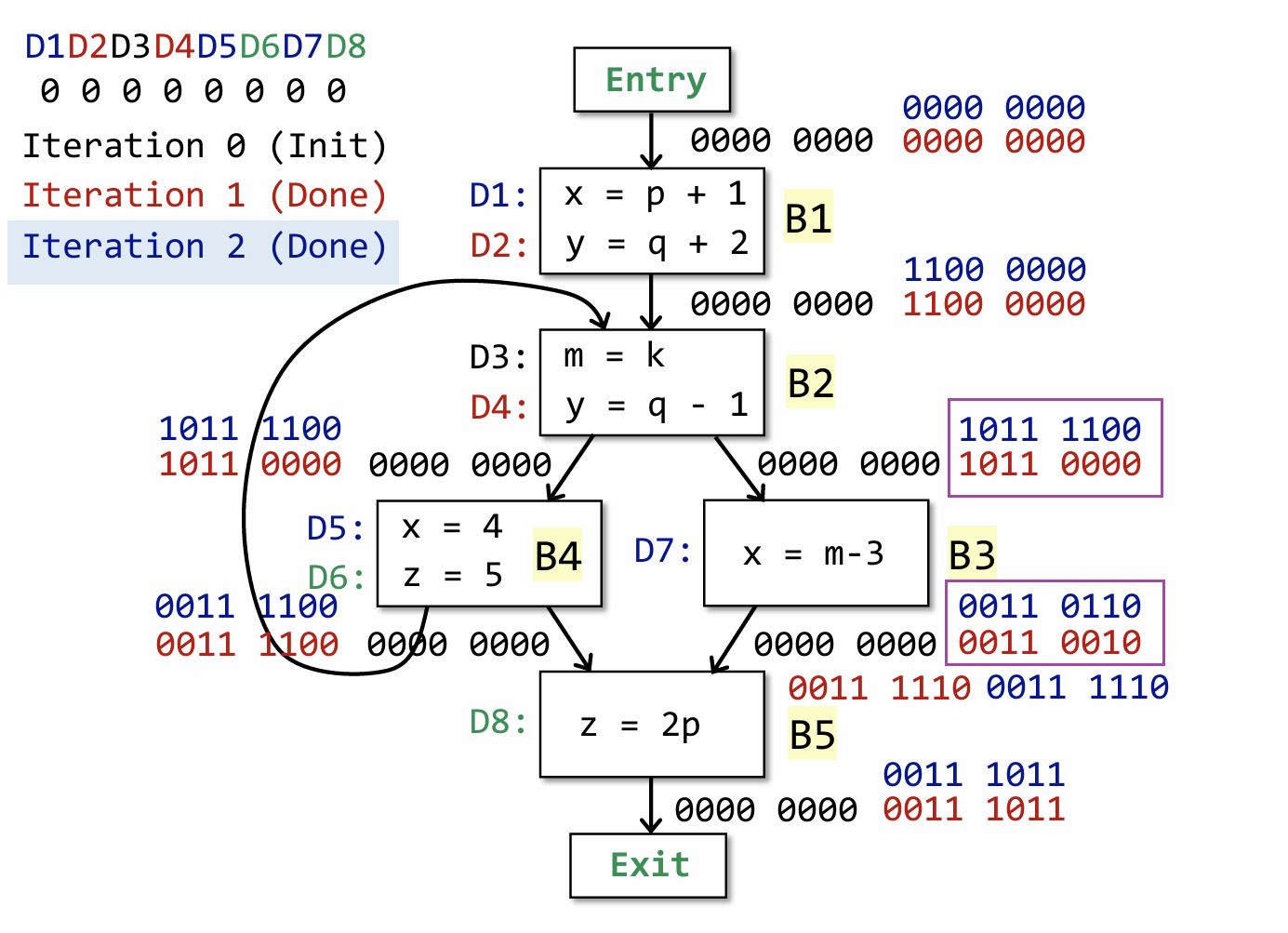
上图为第二次迭代之后的结果，可以发现这一次只有 B2 和 B3 的输出发生了变化，但依然还是满足while循环的条件（只要有一个输出发生变化，必须要重新遍历所有基本块）。

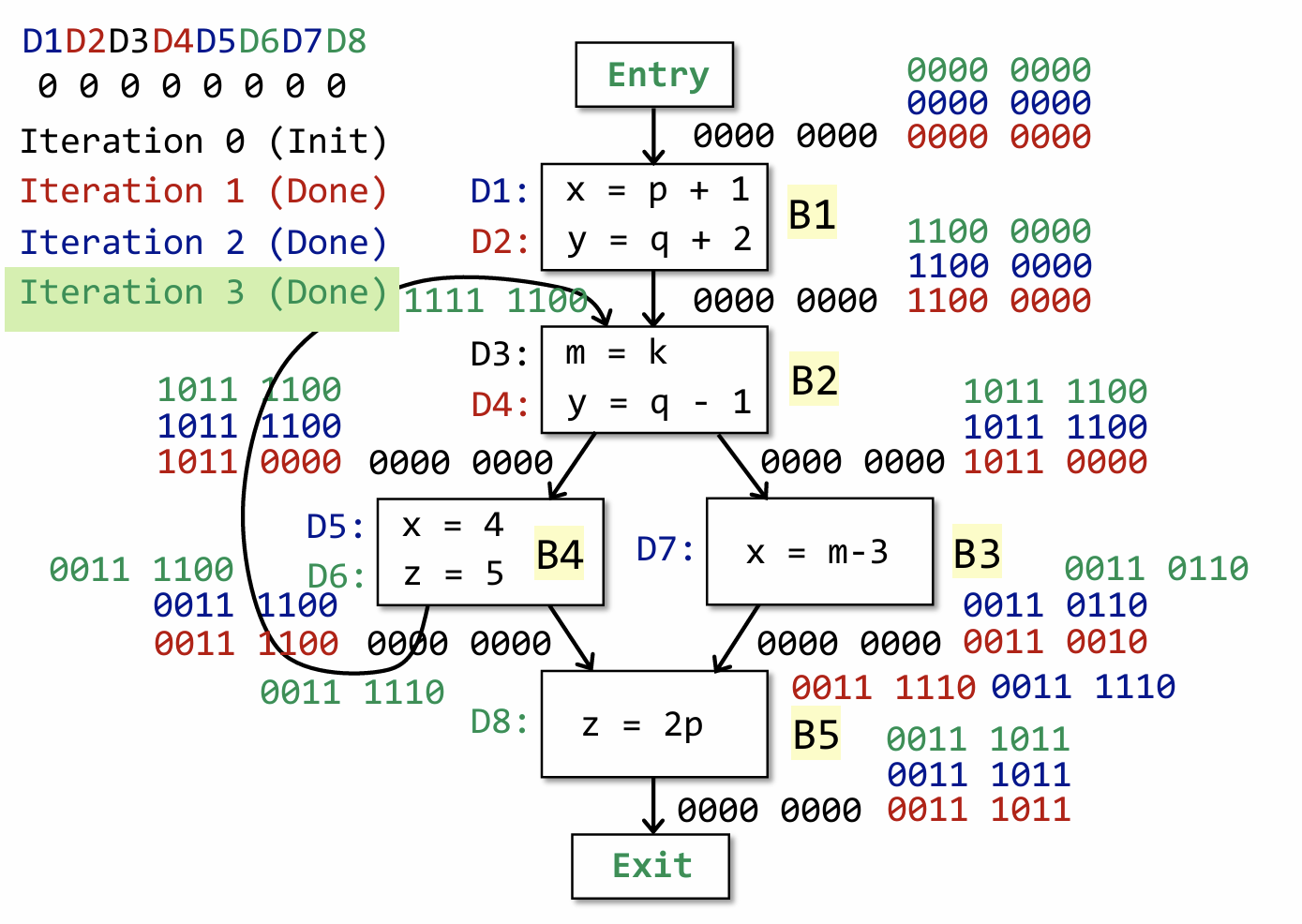
到第三次的时候，会发现所有基本块的输出都没有发生变化了，这意味这我们得到了最终的结果。到这里可能有同学会问，难道后续的迭代遍历 OUT[B] 一定保持不变嘛？这个问题其实可以从公式中找到答案：

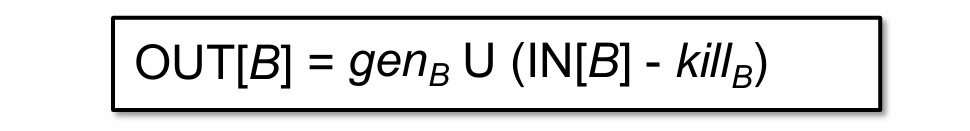
要知道 gen 和 kill 的内容只需我们知道基本块时就可以提前计算好，因为基本块的内容是固定的，相对应的其计算出来的 gen 和 kill 也不会发生变化了，唯一会发生变化的只有 IN[B] 了。因此只有 IN[B] 不会发生变化，输出自然也不会发生变化了。

这里细心的同学可能会注意到，上面随着每次的迭代过程，每一个块的 OUT 的内容只会由 0 变为1，或者还是保持之前的 1，其实可以由我们上面的解释来说明这个问题。

由于一个 CFG 的基本块的所有 OUT 的状态是有限的，且其状态位只能从 0->1，1->1，因此其迭代也必然是有限的。

如果觉得我没有说清楚，也可以参考下面的这张图的解释

总结

这里提两个非常重要的概念：

In each data-flow analysis application, we associate with every program point a data-flow value that represents an abstraction of the set of all possible program states that can be observed for that point.

这个概念稍微绕了点，简单来说就是在数据流分析中把抽象的程序状态用一系列值（比如说我们前面举得例子中的一系列bit位）来表示 OUT[B]。

Data-flow analysis is to find a solution to a set of safe-approximation directed constraints on the IN[s]’s and OUT[s]’s, for all statements s.

• -constraints based on semantics of statements (transfer functions)
• -constraints based on the flows of control

上面这个概念提出了数据分析的目的在于找到一个约束解，比如我们前面举得例子中，迭代到最后所有的输出值都不变了，这些值就是我们最后得到的约束解。